
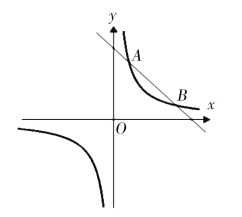
【題目】如圖,雙曲線![]() 與直線
與直線![]() 相交于
相交于![]() ,點P是x軸上一動點.
,點P是x軸上一動點.
(1)求雙曲線![]() 與直線
與直線![]() 的解析式;
的解析式;
(2)當![]() 時,直接寫出x的取值范圍;
時,直接寫出x的取值范圍;
(3)當![]() 是等腰三角形時,求點P的坐標.
是等腰三角形時,求點P的坐標.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() ,
,![]()
![]()
【解析】
(1)根據點A,B在反比例函數圖象上,求出m,k1,再代入直線解析式中,即可得出結論;
(2)根據圖形和點A,B坐標即可得出結論;
(3)設出P坐標,利用等腰三角形的性質分三種情況,建立方程求解即可得出結論.
解:(1)∵A(1,m+2),B(4,m-1)是反比例函數![]() 上,
上,
∴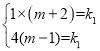 ,解得
,解得![]() ,
,
∴A(1,4),B(4,1)
∵點A,B在直線y2=k2x+b上,
∴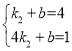 ,解得
,解得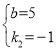 ,
,
∴雙曲線的解析式為y=![]() ,直線的解析式為y=-x+5;
,直線的解析式為y=-x+5;
(2)∵點A(1,m+2),B(4,m-1)是反比例函數和直線的交點坐標,
∴0<x<1或x>4;
(3)設點P(a,0),
則PA2=(a-1)2+42,AB2=18,PB2=(a-4)2+12
①當PA=PB時,(a-1)2+42=(a-4)2+12
解得a=0,
∴P1(0,0),
②當PA=AB時,(a-1)2+42=18,
解得a1=![]() +1,a2=
+1,a2=![]() +1,
+1,
∴P2(![]() +1,0),P3(
+1,0),P3(![]() +1,0),
+1,0),
③當PB=AB時,(a-4)2+12=18,
解得a3=![]() +4,a4=
+4,a4=![]() +4,
+4,
∴P4(![]() +4,0),P5(
+4,0),P5(![]() +4,0),
+4,0),
綜上述,P1(0,0),P2(![]() +1,0),P3(
+1,0),P3(![]() +1,0),P4(
+1,0),P4(![]() +4,0),P5(
+4,0),P5(![]() +4,0).
+4,0).


科目:初中數學 來源: 題型:
【題目】如圖,某攔河壩橫截面原設計方案為梯形ABCD,其中AD∥BC,∠ABC=72°,為了提高攔河壩的安全性,現將壩頂寬度水平縮短10m,壩底寬度水平增加4m,使∠EFC=45°,請你計算這個攔河大壩的高度.(參考數據:sin72°≈![]() ,cos72°≈
,cos72°≈![]() ,tan72°
,tan72°![]() )
)
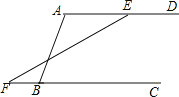
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,五邊形ABCDE中,∠A=140°,∠B=120°,∠E=90°,CP和DP分別是∠BCD、∠EDC的外角平分線,且相交于點P,則∠CPD=__________°.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() ,點
,點![]() 在直線
在直線![]() 上,
上,![]() 與直線
與直線![]() 相交所得的銳角為
相交所得的銳角為![]() ,點
,點![]() 在直線
在直線![]() 上,
上,![]() ,垂足為點
,垂足為點![]() ,與點
,與點![]() 重合,
重合,![]() ,以
,以![]() 為直徑,在
為直徑,在![]() 的右側作半圓
的右側作半圓![]() ,點
,點![]() 是半圓
是半圓![]() 上任意一點.
上任意一點.
(1)發現:連接![]() ,則線段
,則線段![]() 的最大值為____________;
的最大值為____________;
(2)矩形![]() 保持不動,半圓
保持不動,半圓![]() 沿直線
沿直線![]() 向右平移,設平移距離為
向右平移,設平移距離為![]() .思考:點E落在邊
.思考:點E落在邊![]() 上時,求半圓
上時,求半圓![]() 與矩形
與矩形![]() 重合部分的面積
重合部分的面積![]() ;
;
(3)探究:在平移過程中,當半圓![]() 與矩形
與矩形![]() 的邊相切時,直接寫出
的邊相切時,直接寫出![]() 的值(參考數據:
的值(參考數據:![]() 結果保留根號)
結果保留根號)
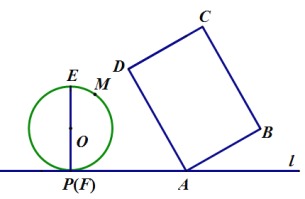
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列等式:![]() ,
,![]() ,
,![]() ,將以上三個等式兩邊分別相加得:
,將以上三個等式兩邊分別相加得:![]() .
.
(1)觀察發現
![]() _________;
_________;
![]() __________.
__________.
(2)初步應用
利用(1)的結論,解決下列問題:
①把![]() 拆成兩個分子為1的正的真分數之差,即
拆成兩個分子為1的正的真分數之差,即![]() __________;
__________;
②把![]() 拆成兩個分子為1的正的真分數之和,即
拆成兩個分子為1的正的真分數之和,即![]() __________.
__________.
(3)深入探究
定義“◆”是一種新的運算,若![]() ,
,![]() ,
,![]() ,則
,則![]() 計算的結果是_________.
計算的結果是_________.
(4)拓展延伸
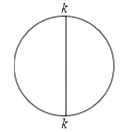
第一次用一條直徑將圓周分成兩個半圓(如圖),在每個分點標上質數![]() ,記2個數的和為
,記2個數的和為![]() ,第二次將兩個半圓都分成
,第二次將兩個半圓都分成![]() 圓,在新產生的分點標相鄰的已標的兩個數的和的
圓,在新產生的分點標相鄰的已標的兩個數的和的![]() ,記4個數的和為
,記4個數的和為![]() ;第三次將四個
;第三次將四個![]() 圓分成
圓分成![]() 圓,在新產生的分點標相鄰的已標的兩個數的和的
圓,在新產生的分點標相鄰的已標的兩個數的和的![]() ,記8個數的和為
,記8個數的和為![]() ;第四次將八個
;第四次將八個![]() 圓分成
圓分成![]() 圓,在新產生的分點標相鄰的已標的兩個數的和的
圓,在新產生的分點標相鄰的已標的兩個數的和的![]() ,記16個數的和為
,記16個數的和為![]() ;……如此進行了
;……如此進行了![]() 次.
次.
①![]() _________(用含
_________(用含![]() 、
、![]() 的代數式表示);
的代數式表示);
②![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,點B的坐標為(0,4),點A是x正半軸上一點,點C在第一象限內,BC⊥AB于點B,∠OAB=∠BAC,當AC=10時,則過點C的反比例函數y=![]() 的比例系數k值為( )
的比例系數k值為( )
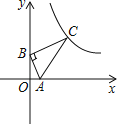
A.32 或 16B.48 或 64C.16 或 64D.32 或 80
查看答案和解析>>
科目:初中數學 來源: 題型:
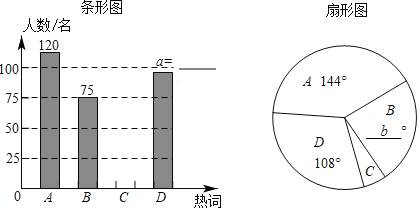
【題目】網絡時代,新興詞匯層出不窮.為了解大眾對網絡詞匯的理解,某興趣小組舉行了一個“我是路人甲”的調查活動:選取四個熱詞A:“硬核人生”,B:“好嗨哦”,C:“雙擊666”,D:“杠精時代”在街道上對流動人群進行了抽樣調查,要求被調查的每位只能勾選一個最熟悉的熱詞,根據調查結果,該小組繪制了如下的兩幅不完整的統計圖,請你根據統計圖提供的信息,解答下列問題:
(1)本次調查中,一共調查了 名路人.
(2)補全條形統計圖;
(3)扇形圖中的b= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=-![]() (x-t)(x-t+6)與直線y=x-1有兩個交點,這兩個交點的縱坐標為m、n.雙曲線y=
(x-t)(x-t+6)與直線y=x-1有兩個交點,這兩個交點的縱坐標為m、n.雙曲線y=![]() 的兩個分支分別位于第二、四象限,則t的取值范圍是( )
的兩個分支分別位于第二、四象限,則t的取值范圍是( )
A.t<0B.0<t<6C.1<t<7D.t<1或t>6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() (點
(點![]() 在點
在點![]() 的左側),對稱軸與
的左側),對稱軸與![]() 軸交于點(3,0),且
軸交于點(3,0),且![]() .
.
(1)求拋物線![]() 的表達式及頂點坐標;
的表達式及頂點坐標;
(2)將拋物線![]() 平移,得到的新拋物線
平移,得到的新拋物線![]() 的頂點為(0,﹣1),拋物線
的頂點為(0,﹣1),拋物線![]() 的對稱軸與兩條拋物線
的對稱軸與兩條拋物線![]() ,
,![]() 圍成的封閉圖形為
圍成的封閉圖形為![]() .直線
.直線![]() 經過點
經過點![]() .若直線
.若直線![]() 與圖形
與圖形![]() 有公共點,求
有公共點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com