
 ,
, ),使得四邊形ABPM為等腰梯形;
),使得四邊形ABPM為等腰梯形;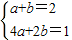 ,
,
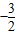 ,b=
,b= ,
,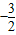 x2+
x2+ x.
x.
 ),∵點M在拋物線上,∴M(t,
),∵點M在拋物線上,∴M(t,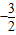 t2+
t2+ t).
t).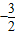 t2+
t2+ t)=
t)= t2-
t2- t+2,BH=PN=
t+2,BH=PN= .
. t2-
t2- t+2=
t+2= ,
, ,
, ,
, )
) ,
, ),使得四邊形ABPM為等腰梯形.
),使得四邊形ABPM為等腰梯形.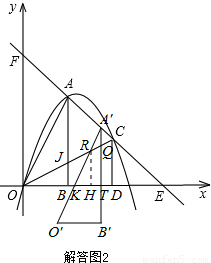
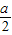 ,
,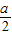 ).
).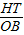 =
=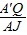
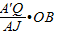 =
=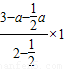 =2-a,
=2-a, A′T=
A′T= (3-a),A′Q=yA′-yQ=(-a+3)-
(3-a),A′Q=yA′-yQ=(-a+3)-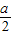 =3-
=3- a.
a.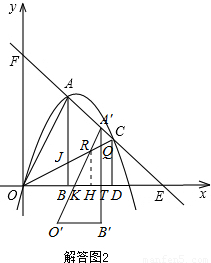
 KT•A′T-
KT•A′T- A′Q•HT
A′Q•HT •
•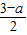 •(3-a)-
•(3-a)- •(3-
•(3- a)•(-a+2)
a)•(-a+2)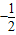 a2+
a2+ a-
a- =
= (a-
(a- )2+
)2+
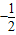 <0,
<0, ,
, ),能使重疊部分面積S取到最大值,最大值為
),能使重疊部分面積S取到最大值,最大值為 .
.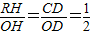 ①
①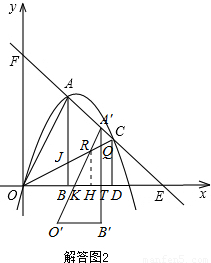
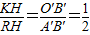 ②
② OH,
OH, OH,KT=OT-OK=a-
OH,KT=OT-OK=a- OH ③
OH ③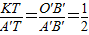 ,
,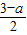 ④
④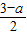 =a-
=a- OH,即OH=2a-2,RH=a-1,所以點R的坐標為R(2a-2,a-1)
OH,即OH=2a-2,RH=a-1,所以點R的坐標為R(2a-2,a-1) •OT•QT-
•OT•QT- •OK•RH
•OK•RH a•
a• a-
a- (1+
(1+ a-
a- )•(a-1)
)•(a-1)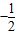 a2+
a2+ a-
a- =
=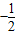 (a-
(a- )2+
)2+
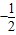 <0,
<0, ,
, ),能使重疊部分面積S取到最大值,最大值為
),能使重疊部分面積S取到最大值,最大值為 .
.
 ,
, =
=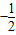 a+
a+ ,
,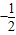 a+
a+ )=
)= a-
a- ,
,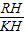 =2,
=2,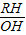 =
=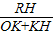 =
= ,
, a-
a- +
+ RH,
RH, •KT•A′T-
•KT•A′T- A′Q•(xQ-xR)
A′Q•(xQ-xR) •
•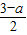 •(3-a)-
•(3-a)- •(3-
•(3- a)•(-a+2)
a)•(-a+2)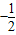 a2+
a2+ a-
a- =
= (a-
(a- )2+
)2+
 <0,
<0, ,
, ),能使重疊部分面積S取到最大值,最大值為
),能使重疊部分面積S取到最大值,最大值為 .
.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
 動點.
動點.查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
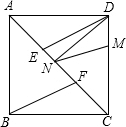
 (2013•石景山區一模)如圖,把兩個全等的Rt△AOB和Rt△ECD分別置于平面直角坐標系xOy中,使點E與點B重合,直角邊OB、BC在y軸上.已知點D (4,2),過A、D兩點的直線交y軸于點F.若△ECD沿DA方向以每秒
(2013•石景山區一模)如圖,把兩個全等的Rt△AOB和Rt△ECD分別置于平面直角坐標系xOy中,使點E與點B重合,直角邊OB、BC在y軸上.已知點D (4,2),過A、D兩點的直線交y軸于點F.若△ECD沿DA方向以每秒| 2 |
查看答案和解析>>
科目:初中數學 來源:2013屆四川德陽市中江縣柏樹中學九年級下學期第一次月考試數學試卷(帶解析) 題型:解答題
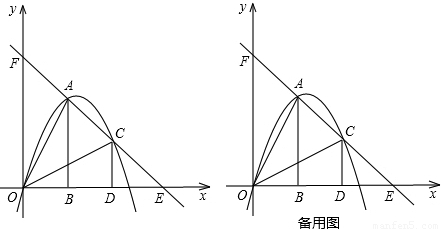
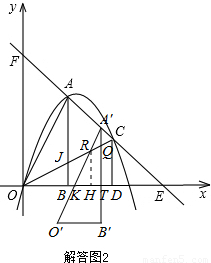
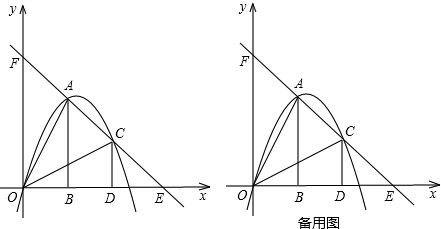
如圖,把兩個全等的Rt△AOB和Rt△COD分別置于平面直角坐標系中,使直角邊OB、OD在x軸上.已知點A(1,2),過A、C兩點的直線分別交x軸、y軸于點E、F.拋物線y=ax2+bx+c經過O、A、C三點.
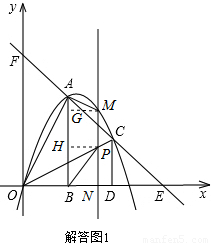
(1)求該拋物線的函數解析式;
(2)點P為線段OC上一個動點,過點P作y軸的平行線交拋物線于點M,交x軸于點N,問是否存在這樣的點P,使得四邊形ABPM為等腰梯形?若存在,求出此時點P的坐標;若不存在,請說明理由.
(3)若△AOB沿AC方向平移(點A始終在線段AC上,且不與點C重合),△AOB在平移過程中與△COD重疊部分面積記為S.試探究S是否存在最大值?若存在,求出這個最大值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源:2012-2013學年四川德陽市九年級下學期第一次月考試數學試卷(解析版) 題型:解答題
如圖,把兩個全等的Rt△AOB和Rt△COD分別置于平面直角坐標系中,使直角邊OB、OD在x軸上.已知點A(1,2),過A、C兩點的直線分別交x軸、y軸于點E、F.拋物線y=ax2+bx+c經過O、A、C三點.
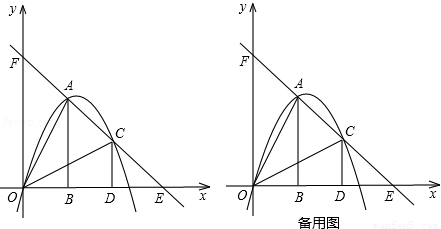
(1)求該拋物線的函數解析式;
(2)點P為線段OC上一個動點,過點P作y軸的平行線交拋物線于點M,交x軸于點N,問是否存在這樣的點P,使得四邊形ABPM為等腰梯形?若存在,求出此時點P的坐標;若不存在,請說明理由.
(3)若△AOB沿AC方向平移(點A始終在線段AC上,且不與點C重合),△AOB在平移過程中與△COD重疊部分面積記為S.試探究S是否存在最大值?若存在,求出這個最大值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com