
【題目】如圖1,拋物線y=ax2+b的頂點坐標為(0,﹣1),且經過點A(﹣2,0). 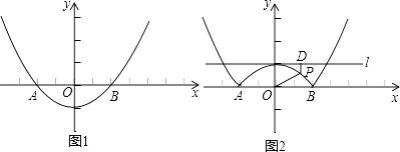
(1)求拋物線的解析式;
(2)若將拋物線y=ax2+b中在x軸下方的圖象沿x軸翻折到x軸上方,x軸上方的圖象保持不變,就得到了函數y=|ax2+b|圖象上的任意一點P,直線l是經過(0,1)且平行與x軸的直線,過點P作直線l的垂線,垂足為D,猜想并探究:PO與PD的差是否為定值?如果是,請求出此定值;如果不是,請說明理由. (注:在解題過程中,如果你覺得有困難,可以閱讀下面的材料)
附閱讀材料:
① 在平面直角坐標系中,若A、B兩點的坐標分別為A(x1 , y1),B(x2 , y2),則A,B兩點間的距離為|AB|= ![]() ,這個公式叫兩點間距離公式.
,這個公式叫兩點間距離公式.
例如:已知A,B兩點的坐標分別為(﹣1,2),(2,﹣2),則A,B兩點間的距離為|AB|= ![]() =5.
=5.
② 因式分解:x4+2x2y2+y4=(x2+y2)2 .
【答案】
(1)解:根據題意設拋物線解析式為y=ax2﹣1,
將點A(﹣2,0)代入,得:4a﹣1=0,
解得:a= ![]() ,
,
∴拋物線的解析式為y= ![]() x2﹣1
x2﹣1
(2)解:如圖,
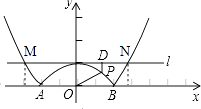
根據題意,當﹣2≤x≤2時,y=﹣ ![]() x2+1;
x2+1;
當x<﹣2或x>2時,y= ![]() x2﹣1;
x2﹣1;
由 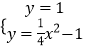 可得點M(﹣2
可得點M(﹣2 ![]() ,1)、點N(2
,1)、點N(2 ![]() ,1),
,1),
① 當﹣2≤x≤2時,設點P坐標為(a,﹣ ![]() a2+1),
a2+1),
則PO﹣PD= ![]() ﹣[1﹣(﹣
﹣[1﹣(﹣ ![]() a2+1)]
a2+1)]
= ![]() a2+1﹣
a2+1﹣ ![]() a2
a2
=1;
②當﹣2 ![]() ≤x<﹣2或2
≤x<﹣2或2 ![]() 時,設點P的坐標為(a,
時,設點P的坐標為(a, ![]() a2﹣1),
a2﹣1),
則PO﹣PD= ![]() ﹣[1﹣(
﹣[1﹣( ![]() a2﹣1)]
a2﹣1)]
= ![]() a2+1﹣2+
a2+1﹣2+ ![]() a2
a2
= ![]() a2﹣1;
a2﹣1;
③當x<﹣2 ![]() 或x>2
或x>2 ![]() 時,設點P的坐標為(a,
時,設點P的坐標為(a, ![]() a2﹣1),
a2﹣1),
則PO﹣PD= ![]() ﹣[(
﹣[( ![]() a2﹣1)﹣1]
a2﹣1)﹣1]
= ![]() a2+1﹣
a2+1﹣ ![]() a2+2
a2+2
=3;
綜上,當x<﹣2 ![]() 、﹣2≤x≤2或x>2
、﹣2≤x≤2或x>2 ![]() 時,PO與PD的差為定值
時,PO與PD的差為定值
【解析】(1)待定系數法求解可得;(2)先根據題意表示出翻折后拋物線解析式,再求出y=1時x的值,繼而可分﹣2≤x≤2、﹣2 ![]() ≤x<﹣2或2
≤x<﹣2或2 ![]() 、x<﹣2
、x<﹣2 ![]() 或x>2
或x>2 ![]() 三種情況,根據兩點間距離公式列式表示出PO與PD的差即可得出答案.
三種情況,根據兩點間距離公式列式表示出PO與PD的差即可得出答案.
【考點精析】根據題目的已知條件,利用二次函數圖象以及系數a、b、c的關系和坐標與圖形變化-對稱的相關知識可以得到問題的答案,需要掌握二次函數y=ax2+bx+c中,a、b、c的含義:a表示開口方向:a>0時,拋物線開口向上; a<0時,拋物線開口向下b與對稱軸有關:對稱軸為x=-b/2a;c表示拋物線與y軸的交點坐標:(0,c);關于x軸對稱的點的特征:兩個點關于x軸對稱時,它們的坐標中,x相等,y的符號相反,即點P(x,y)關于x軸的對稱點為P’(x,-y);關于y軸對稱的點的特征:兩個點關于y軸對稱時,它們的坐標中,y相等,x的符號相反,即點P(x,y)關于y軸的對稱點為P’(-x,y).


 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案科目:初中數學 來源: 題型:
【題目】如圖,∠AOB=120°,OC是∠AOB內部任意一條射線,OD、OE分別是∠AOC、∠BOC的角平分線,下列敘述正確的是( )
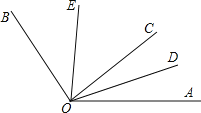
A. ∠DOE的度數不能確定 B. ∠AOD=![]() ∠EOC
∠EOC
C. ∠AOD+∠BOE=60° D. ∠BOE=2∠COD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠BAC=45°,AD⊥BC于點D,BE⊥AC于點E,且與AD交于點F.G是邊AB的中點,連接EG交AD于點H.
(1)求證:△AEF≌△BEC;
(2)求證:CD=![]() AF;
AF;
(3)若BD=2,求AH的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】.某區在實施居民用水額定管理前,對居民生活用水情況進行了調查,下表是通過簡單隨機抽樣獲得的50個家庭去年月平均用水量![]() 單位:噸
單位:噸![]() ,并將調查數據進行如下整理:
,并將調查數據進行如下整理:

頻數分布表
分組 | 劃記 | 頻數 |
| 正正 | 11 |
|
| 19 |
| ||
合計 |
| 2 50 |
![]() 把上面頻數分布表和頻數分布直方圖補充完整;
把上面頻數分布表和頻數分布直方圖補充完整;
![]() 從直方圖中你能得到什么信息?
從直方圖中你能得到什么信息? ![]() 寫出兩條即可
寫出兩條即可![]() ;
;
![]() 為了鼓勵節約用水,要確定一個用水量的標準,超出這個標準的部分按
為了鼓勵節約用水,要確定一個用水量的標準,超出這個標準的部分按![]() 倍價格收費,若要使
倍價格收費,若要使![]() 的家庭收費不受影響,你覺得家庭月均用水量應該定為多少?為什么?
的家庭收費不受影響,你覺得家庭月均用水量應該定為多少?為什么?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,OD垂直弦AC于點E,且交⊙O于點D,過點D作⊙O的切線與BA的延長線相交于點F,下列結論不一定正確的是( ) 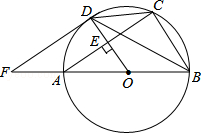
A.∠CDB=∠BFD
B.△BAC∽△OFD
C.DF∥AC
D.OD=BC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】決心試一試,請閱讀下列材料:計算:![]()
解法一:原式=![]()
=![]()
=![]()
解法二:原式=![]()
=![]()
=![]()
=![]()
解法三:原式的倒數為:![]()
=![]()
=﹣20+3﹣5+12
=﹣10
故原式 =![]()
上述得出的結果不同,肯定有錯誤的解法,你認為解法 是錯誤的,在正確的解法中,你認為解法 最簡捷.然后請解答下列問題,計算:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按圖中方式用火柴棒搭正方形
![]()
①搭1個正方形需要 根火柴棒;
②搭2個正方形需要 根火柴棒,搭3個正方形需要 根火柴棒;
③搭10個這樣的正方形需要多少根火柴棒;
④搭100個這樣的正方形需要多少根火柴棒?
⑤如果用x表示所搭正方形的個數,那么搭x個這樣的正方形需要多少根火柴棒?與同伴交流。
⑥根據你的計算方法,搭200個這樣的正方形需要多少根火柴棒?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com