
【題目】某商店分兩次購進A,B兩種商品進行銷售,兩次購進同一種商品的進價相同,具體情況如下表所示:
購進數量(件) | 購進所需費用(元) | ||
A | B | ||
第一次 | 20 | 30 | 2800 |
第二次 | 30 | 20 | 2200 |
(1)求A、B兩種商品每件的進價分別是多少元?
(2)商場決定A種商品以每件30元出售,B種商品以每件100元出售.為滿足市場需求,需購進A、B兩種商品共1000件,且A種商品的數量不少于B種商品數量的4倍,請你求出獲利最大的進貨方案,并確定最大利潤.
【答案】(1)A、B兩種商品每件的進價分別是20元,80元;(2)a=800時,m的最大值為12000元.
【解析】
(1)設A種商品每件的進價為x元,B種商品每件的進價為y元,根據兩次進貨情況表,可得出關于x、y的二元一次方程組,解之即可得出結論;
(2))設A商品a件,B商品(1000﹣a)件,利潤為m元,根據題意列出不等式組,解之即可得出a的取值范圍,根據總利潤=單件利潤×購進數量,可得出m和a的函數關系式,再根據一次函數的性質即可解決最值問題.
(1)設A、B兩種商品每件的進價分別是x元,y元
根據題意得:![]()
解得:![]()
答A、B兩種商品每件的進價分別是20元,80元.
(2)設A商品a件,B商品(1000﹣a)件,利潤為m元.
根據題意得: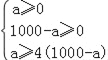
解得:800≤a≤1000
m=(30﹣20)a+(100﹣80)(1000﹣a)=20000﹣10a
∵k=﹣10<0
∴m隨a的增大而減小
∴a=800時,m的最大值為12000元.


 快樂暑假暑假能力自測中西書局系列答案
快樂暑假暑假能力自測中西書局系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,△ABC的位置如圖所示.
(1)頂點A關于x軸對稱的點A′的坐標(____________),頂點B的坐標(____________),頂點C關于原點對稱的點C′的坐標(____________).
(2)△ABC的面積為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰三角形紙片ABC中,AB=AC=10,BC=12,將此等腰三角形紙片沿底邊BC上的高AD剪成兩個全等的三角形,用這兩個三角形拼成一個平行四邊形,則所拼出的所有平行四邊形中最長的對角線的長是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究題:![]() =___________,
=___________,![]() =___________,
=___________,![]() =___________,
=___________,
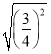 =_________,
=_________,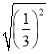 =__________,
=__________,![]() =___________,
=___________,
根據計算結果,回答:
(1)![]() 一定等于
一定等于![]() 嗎?你發現其中的規律了嗎?請你用數學語言描述出來。
嗎?你發現其中的規律了嗎?請你用數學語言描述出來。
(2)利用你總結的規律,計算:
①若![]() ,則
,則![]() =_____________;
=_____________;
②![]() =______________________;
=______________________;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]() 經過點A(
經過點A(![]() ,0),B(
,0),B(![]() ,0),且與y軸相交于點C.
,0),且與y軸相交于點C.
(1)求這條拋物線的表達式;
(2)求∠ACB的度數;
(3)設點D是所求拋物線第一象限上一點,且在對稱軸的右側,點E在線段AC上,且DE⊥AC,當△DCE與△AOC相似時,求點D的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題滿分10分)
如圖,在□ABCD中,以點A為圓心,AB長為半徑畫弧交AD于點F;再分別以點B、F為圓心,大于![]() BF的相同長為半徑畫弧,兩弧交于點P;連接AP并延長交BC于點E,連接EF,則所得四邊形ABEF是菱形.
BF的相同長為半徑畫弧,兩弧交于點P;連接AP并延長交BC于點E,連接EF,則所得四邊形ABEF是菱形.
(1)根據以上尺規作圖的過程,求證四邊形ABEF是菱形;
(2)若菱形ABEF的周長為16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數軸上點A表示a,點B表示b,且a,b滿足![]()
(1)x表示a+b的整數部分,y表示a+b的小數部分,則x= y = ;
(2)若點A與點C之間的距離表示AC,點B與點C之間的距離表示BC,請在數軸上找一點C,使得AC=2BC,求點C在數軸上表示的數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在矩形ABCD中,AD=3,CD=4,點E在CD上,且DE=1.



(1)感知:如圖①,連接AE,過點E作EF丄AE,交BC于點F,連接AE,易證:△ADE≌△ECF(不需要證明);
(2)探究:如圖②,點P在矩形ABCD的邊AD上(點P不與點A、D重合),連接PE,過點E作EF⊥PE,交BC于點F,連接PF.求證:△PDE和△ECF相似;
(3)應用:如圖③,若EF交AB于點F,EF丄PE,其他條件不變,且△PEF的面積是6,則AP的長為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com