
【題目】將一副三角板中的兩塊直角三角尺的直角頂點C按如圖所示的方式疊放在一起(其中,![]() ,
,![]() ;
;![]() ).
).
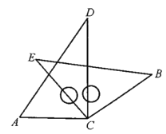
(1)①若![]() ,則
,則![]() 的度數為_____________;
的度數為_____________;
②若![]() ,則
,則![]() 的度數為_____________.
的度數為_____________.
(2)由(1)猜想![]() 與
與![]() 的數量關系,并說明理由.
的數量關系,并說明理由.
(3)當![]() 且點E在直線AC的上方時,這兩塊三角尺是否存在一組邊互相平行?若存在,請寫出
且點E在直線AC的上方時,這兩塊三角尺是否存在一組邊互相平行?若存在,請寫出![]() 角度所有可能的值(不必說明理由);若不存在,請說明理由.
角度所有可能的值(不必說明理由);若不存在,請說明理由.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() ,理由詳見解析;(3)∠ACE=45°或30°或120°或135°或165°
,理由詳見解析;(3)∠ACE=45°或30°或120°或135°或165°
【解析】
(1)①先求出∠ACE,即可求出∠ACB;
②先求出∠ACE,即可求出∠DCE;
(2)根據題意可得![]() ,
,![]() ,從而求出
,從而求出![]() 與
與![]() 的數量關系;
的數量關系;
(3)根據平行線的判定定理和邊的平行關系分類討論,然后畫出對應的圖形即可得出結論.
解:(1)①∵![]() ,∠ACD=∠BCE=90°
,∠ACD=∠BCE=90°
∴∠ACE=∠ACD-∠DCE=45°
∴∠ACB=∠ACE+∠BCE=135°
故答案為:![]() .
.
②∵![]() ,∠ACD=∠BCE=90°
,∠ACD=∠BCE=90°
∴∠ACE=∠ACB-∠BCE=50°
∴∠DCE=∠ACD-∠ACE =40°
故答案為:![]() .
.
(2)![]() .理由如下
.理由如下
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]()
∴![]() .
.
(3)①當![]() 時,
時,
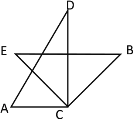
∵![]()
∴![]()
∴![]() ,
,
②當![]() 時,設CE與AD交于點F,如下圖所示
時,設CE與AD交于點F,如下圖所示

∵∠A=60°,∠BCE=90°
∴∠AFC=180°-∠ACE-∠A=90°
∴∠AFC=∠BCE
∴![]() .
.
③當![]() 時,如下圖所示
時,如下圖所示
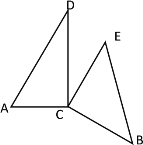
∵∠ACD=90°,∠D=30°
∴∠DCE=∠ACE-∠ACD=30°
∴∠DCE=∠D
∴![]() .
.
④當![]() 時,如下圖所示
時,如下圖所示

∵∠ACD=90°,∠E=45°
∴∠DCE=∠ACE-∠ACD=45°
∴∠DCE=∠E
∴![]() .
.
⑤當![]() 時,過點C作CG∥AD,如下圖所示
時,過點C作CG∥AD,如下圖所示

∴∠D=∠DCG=30°
∵∠ACD=90°,∠E=45°
∴∠GCE=∠ACE-∠ACD-∠DCG=45°
∴∠E=∠GCE
∴BE∥CG
∴![]() .
.
綜上所述:∠ACE=45°或30°或120°或135°或165°.


科目:初中數學 來源: 題型:
【題目】如圖,在長方形ABCD中,AC是對角線.將長方形ABCD繞點B順時針旋轉90°到長方形GBEF位置,H是EG的中點.若AB=6,BC=8,則線段CH的長為( )
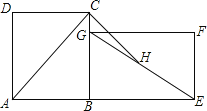
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,用3根火柴可拼成1個三角形,5根火柴可拼成2個三角形,7根火柴可拼成3個三角形……,按這個規律拼,用99根火柴可拼成____個三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
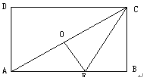
【題目】如圖,點O是矩形ABCD的中心,E是AB上的點,沿CE折疊后,點B恰好與點O重合,若BC=3,則折痕CE的長為( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中數學 來源: 題型:
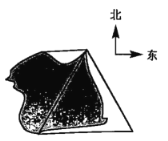
【題目】如圖所示,某湖上風景區有兩個觀望點A,C和兩個度假村B、D;度假村D在C正西方向,度假村B在C的南偏東![]() 方向,度假村B到兩個觀望點的距離都等于2km.
方向,度假村B到兩個觀望點的距離都等于2km.
(1)在圖中標出A、B、C、D的位置,并寫出道路CD與CB的夾角.
(2)如果度假村D到C是直公路,長為1km,D到A是環湖路,度假村B到兩個觀望點的總路程等于度假村D到兩個觀望點的總路程.求出環湖路的長.
(3)根據題目中的條件,能夠判定![]() 嗎?若能,請寫出判斷過程;若不能,請你添加一個條件,判定
嗎?若能,請寫出判斷過程;若不能,請你添加一個條件,判定![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
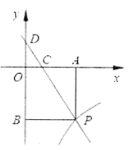
【題目】已知:如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() (
(![]() )的圖象交于點
)的圖象交于點![]() .
.![]() 軸于點
軸于點![]() ,
,![]() 軸于點
軸于點![]() . 一次函數的圖象分別交
. 一次函數的圖象分別交![]() 軸、
軸、![]() 軸于點
軸于點![]() 、點
、點![]() ,且
,且![]() ,
,![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)求一次函數與反比例函數的解析式;
(3)根據圖象寫出當![]() 取何值時,一次函數的值小于反比例函數的值?
取何值時,一次函數的值小于反比例函數的值?
查看答案和解析>>
科目:初中數學 來源: 題型:
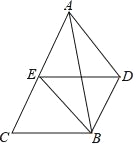
【題目】如圖,已知DB∥AC,E是AC的中點,DB=AE,連結AD、BE.
(1)求證:四邊形DBCE是平行四邊形;
(2)若要使四邊形ADBE是矩形,則△ABC應滿足什么條件?說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某單位欲從內部招聘管理人員一名,對甲、乙、丙三名候選人進行了筆試和面試兩項測試,三人的測試成績如下表所示:
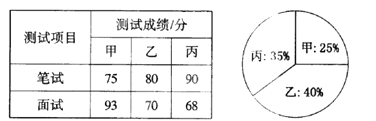
根據錄用程序,組織200名職工對三人利用投票推薦的方式進行民主評議,三人得票率(沒有棄權票,每位職工只能推薦1人)如上圖所示,每得一票記作1分.
(l)請算出三人的民主評議得分;
(2)如果根據三項測試的平均成績確定錄用人選,那么誰將被錄用(精確到 0.01 )?
(3)根據實際需要,單位將筆試、面試、民主評議三項測試得分按 4 : 3 : 3 的比例確定個人成績,那么誰將被錄用?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com