
【題目】如圖,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.

(1)若∠DEC=25°,求∠B的度數;
(2)求證:直線AD是線段CE的垂直平分線.
【答案】(1)∠B=40°;(2)見解析.
【解析】
(1)依據角平分線的的性質,即可得出DE=DC,進而得出∠BDE的度數,再根據DE⊥AB,即可得出∠B的度數;
(2)依據全等三角形的對應邊相等,即可得到AE=AC,ED=DC,進而得到點D在CE的垂直平分線上,點A在CE的垂直平分線上.
(1)∵∠ACB=90°,AD平分∠BAC,DE⊥AB,
∴DE=DC,
∴∠DEC=∠DCE=25°,
∴∠BDE=50°,
又∵DE⊥AB,
∴Rt△BDE中,∠B=90°﹣∠BDE=90°﹣50°=40°;
(2)∵DE⊥AB,
∴∠AED=90°=∠ACB,
又∵DE=DC,AD=AD,
∴△AED≌△ACD(HL),
∴ED=DC,AE=AC,
∴點D在CE的垂直平分線上,點A在CE的垂直平分線上,
∴直線AD是線段CE的垂直平分線.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系中,![]() 點坐標
點坐標![]() ,且
,且![]() ,
,![]() 滿足
滿足![]()

(1)如圖(1)當![]() 為等腰直角三角形時;
為等腰直角三角形時;
①點![]() 坐標為__________;點
坐標為__________;點![]() 坐標為__________.
坐標為__________.
②在(1)的條件下,分別以![]() 和
和![]() 為邊作等邊
為邊作等邊![]() 和等邊
和等邊![]() ,連結
,連結![]() ,求
,求![]() 的度數.
的度數.
(2)如圖(2),過點![]() 作
作![]() 軸于點
軸于點![]() ,點
,點![]() 為
為![]() 軸正半軸上一點,
軸正半軸上一點,![]() 為
為![]() 延長線上一點,以
延長線上一點,以![]() 為直角邊作等腰直角三角形
為直角邊作等腰直角三角形![]() ,
,![]() ,過點
,過點![]() 作
作![]() 軸交
軸交![]() 于點
于點![]() ,連結
,連結![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
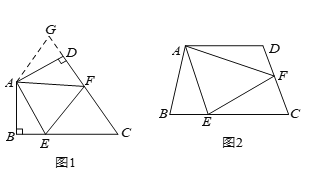
【題目】如圖(![]() ),在四邊形
),在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 上的點,且
上的點,且![]() .探究圖中線段
.探究圖中線段![]() ,
,![]() ,
,![]() 之間的數量關系.小王同學探究此問題的方法是,延長
之間的數量關系.小王同學探究此問題的方法是,延長![]() 到點
到點![]() ,使
,使![]() ,連接
,連接![]() ,先證明
,先證明![]() ≌
≌![]() ,再證明
,再證明![]() ≌
≌![]() ,可得出結論,他的結論應該是__________.
,可得出結論,他的結論應該是__________.
如圖(![]() ),若在四邊形
),若在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 上的點,且
上的點,且![]() ,上述結論是否仍然成立,并說明理由.
,上述結論是否仍然成立,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知:∠MON=30°,點A1、A2、A3…在射線ON上,點B1、B2、B3…在射線OM上,△A1B1A2、△A2B2A3、△A3B3A4…均為等邊三角形,若OA1=1,則△A6B6A7的邊長為( )

A. 16B. 32C. 64D. 128
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在△ABC中,BE、CF分別是AC、AB兩邊上的高,在BE上截取BD=AC,在CF的延長線上截取CG=AB,連接AD、AG.
(1)求證:AD=AG;
(2)AD與AG的位置關系如何,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校決定在4月7日開展“世界無煙日”宣傳活動,活動有A.社區板報、B.集會演講、C.喇叭廣播、D.發宣傳畫四種宣傳方式.學校圍繞“你最喜歡的宣傳方式是什么?”在全校學生中進行隨機抽樣調查(四個選項中必選且只選一項),根據調查統計結果,繪制了如下兩種不完整的統計圖表:

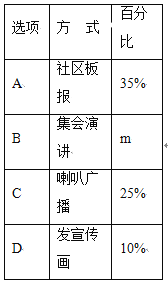
請結合統計圖表,回答下列問題:
(1)本次抽查的學生共______人,m=____________,并將條形統計圖補充完整;
(2)若該校學生有1500人,請你估計該校喜歡“集會演講”這項宣傳方式的學生約有多少人?
(3)學校采用抽簽方式讓每班在A、B、C、D四種宣傳方式中隨機抽取兩種進行展示,請用樹狀圖或列表法求某班所抽到的兩種方式恰好是“集會演講”和“喇叭廣播”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在△ABC中,∠ACB=90°,點P是線段AC上一點,過點A作AB的垂線,交BP的延長線于點M,MN⊥AC于點N,PQ⊥AB于點Q,AQ=MN. 求證:
(1)△APM是等腰三角形;
(2)PC=AN.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,點D為一等腰直角三角形紙片的斜邊AB的中點,E是BC邊上的一點,將這張紙片沿DE翻折成如圖②,使BE與AC邊相交于點F,若圖①中AB=![]() ,則圖②中△CEF的周長為______.
,則圖②中△CEF的周長為______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com