
 DB.
DB.

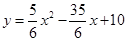 ;(2)∠ECB的大小不變.90°;(3)證明見解析;(4)∠APC>45°.
;(2)∠ECB的大小不變.90°;(3)證明見解析;(4)∠APC>45°.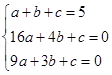 ,解得:
,解得: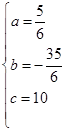 ;
;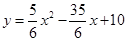 ;
; DB,
DB, BD,連接CF、BF.
BD,連接CF、BF.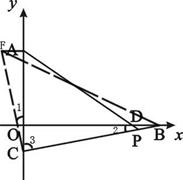


科目:初中數學 來源:不詳 題型:解答題
 )秒.
)秒.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
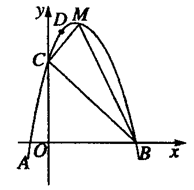
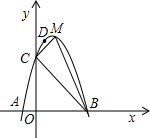
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
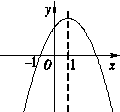
 ,該產品的外地銷售量y2(萬臺)與外地廣告費用t(萬元)之間的函數關系可用如圖所示的拋物線和線段AB來表示,其中點A為拋物線的頂點.
,該產品的外地銷售量y2(萬臺)與外地廣告費用t(萬元)之間的函數關系可用如圖所示的拋物線和線段AB來表示,其中點A為拋物線的頂點.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
A. |
B.當 時,y隨x的增大而增大 時,y隨x的增大而增大 |
C. |
D. 是一元二次方程 是一元二次方程 的一個根 的一個根 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
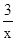 的交點的橫坐標x0的取值范圍是( )
的交點的橫坐標x0的取值范圍是( )| A.0<x0<1 |
| B.1<x0<2 |
| C.2<x0<3 |
| D.﹣1<x0<0 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com