
【題目】如圖,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 和點
和點![]() .(1)已知點
.(1)已知點![]() 在第一象限的拋物線上,則點
在第一象限的拋物線上,則點![]() 的坐標是_______.(2)在(l)的條件下連接
的坐標是_______.(2)在(l)的條件下連接![]() ,
,![]() 為拋物線上一點且
為拋物線上一點且![]()
![]() ,則點
,則點![]() 的坐標是_______.
的坐標是_______.

【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)由題意把![]() 點坐標
點坐標![]() 代入函數(shù)解析式求出m,并由
代入函數(shù)解析式求出m,并由![]() 點在第一象限判斷點
點在第一象限判斷點![]() 的坐標;
的坐標;
(2)利用相似三角形相關(guān)性質(zhì)判定![]() ≌
≌![]() ,并根據(jù)題意設(shè)
,并根據(jù)題意設(shè)![]() ,則
,則![]() ,表示P,把
,表示P,把![]() 代入函數(shù)解析式從而得解.
代入函數(shù)解析式從而得解.
解:(1)把![]() 點坐標
點坐標![]() 代入函數(shù)解析式
代入函數(shù)解析式![]() 得
得![]()
解得![]()
∵![]() 點在第一象限
點在第一象限
∴![]()
∴![]()
∴![]()
(2)∵![]() (
(![]() 作為特殊角,處理方法是作其補角
作為特殊角,處理方法是作其補角![]() )
)
∴過點![]() 作
作![]() 延長線于點
延長線于點![]()
∵![]() ,
,![]()
∴![]() 為等腰直角三角形
為等腰直角三角形
∴![]() (因為
(因為![]() ,
,![]() ,所以考慮構(gòu)造一線三垂直,水平豎直作垂線)
,所以考慮構(gòu)造一線三垂直,水平豎直作垂線)
∴過點![]() 作
作![]() 軸于點
軸于點![]() ,
,![]() 于點
于點![]()
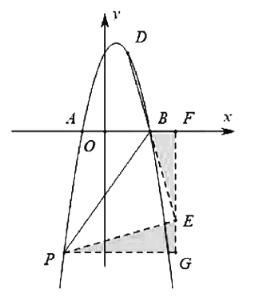
∴![]() ≌
≌![]()
∵![]()
∴![]()
∴![]()
設(shè):![]() ,則
,則![]()
∴![]()
∴![]() (注意咱們設(shè)
(注意咱們設(shè)![]() ,
,![]() 為整數(shù),
為整數(shù),![]() 點在第三象限,橫縱坐標為負數(shù),所以
點在第三象限,橫縱坐標為負數(shù),所以![]() 點的坐標表示要注意正負!)
點的坐標表示要注意正負!)
把![]() 代入函數(shù)解析式得
代入函數(shù)解析式得![]()
解得![]() 或6(
或6(![]() 舍去)
舍去)
∴![]()
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() .將
.將![]() 向內(nèi)翻折,點
向內(nèi)翻折,點 ![]() 落在
落在![]() 上,記為
上,記為![]() ,折痕為
,折痕為![]() .若將
.若將![]() 沿
沿![]() 向內(nèi)翻折,點
向內(nèi)翻折,點![]() 恰好 落在
恰好 落在![]() 上,記為
上,記為![]() ,則
,則![]() 的長為( )
的長為( )
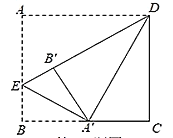
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】定義:幾個全等的正多邊形依次有一邊重合,排成一圈,中間可以圍成一個正多邊形,我們稱作正多邊形的環(huán)狀連接。如圖,我們可以看作正六邊形的環(huán)狀連接,中間圍成一個邊長相等的正六邊形;若正八邊形作環(huán)狀連接,中間可以圍的正多邊形的邊數(shù)為;

若正八邊形作環(huán)狀連接,中間可以圍的正多邊形的邊數(shù)為________,若邊長為1的正n邊形作環(huán)狀連接,中間圍成的是等邊三角形,則這個環(huán)狀連接的外輪廓長為_________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
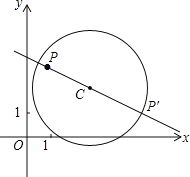
【題目】在平面直角坐標系xOy中,⊙C的半徑為r,P是與圓心C不重合的點,點P關(guān)于⊙C的限距點的定義如下:若P′為直線PC與⊙C的一個交點,滿足r≤PP′≤2r,則稱P′為點P關(guān)于⊙C的限距點,如圖為點P及其關(guān)于⊙C的限距點P′的示意圖.
(1)當(dāng)⊙O的半徑為1時.
①分別判斷點M(3,4),N(![]() ,0),T(1,
,0),T(1,![]() )關(guān)于⊙O的限距點是否存在?若存在,求其坐標;
)關(guān)于⊙O的限距點是否存在?若存在,求其坐標;
②點D的坐標為(2,0),DE,DF分別切⊙O于點E,點F,點P在△DEF的邊上.若點P關(guān)于⊙O的限距點P′存在,求點P′的橫坐標的取值范圍;
(2)保持(1)中D,E,F三點不變,點P在△DEF的邊上沿E→F→D→E的方向運動,⊙C的圓心C的坐標為(1,0),半徑為r,請從下面兩個問題中任選一個作答.
問題1:若點P關(guān)于⊙C的限距點P′存在,且P′隨點P的運動所形成的路徑長為πr,則r的最小值為__________.
問題2:若點P關(guān)于⊙C的限距點P′不存在,則r的取值范圍為_________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
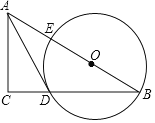
【題目】如圖,在Rt△ABC中,點O在斜邊AB上,以O(shè)為圓心,OB為半徑作圓,分別與BC,AB相交于點D,E,連結(jié)AD.已知∠CAD=∠B,
(1)求證:AD是⊙O的切線.
(2)若BC=8,tanB=![]() ,求⊙O 的半徑.
,求⊙O 的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形ABCD是由三個全等矩形拼成的,AC與DE、EF、FG、HG、HB分別交于點P、Q、K、M、N,設(shè)△EPQ、△GKM、△BNC的面積依次為S1、S2、S3.若S1+S3=30,則S2的值為( ).
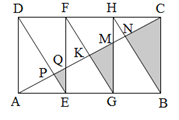
A.6B.8
C.10D.12
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線![]() (
(![]() ).
).
(1)寫出拋物線頂點的縱坐標 (用含a的代數(shù)式表示);
(2)若該拋物線與x軸的兩個交點分別為點A和點B,且點A在點B的左側(cè),AB=4.
①求a的值;
②記二次函數(shù)圖象在點A,B之間的部分為W(含點A和點B),若直線![]() (
(![]() )經(jīng)過(1,-1),且與圖形W有公共點,結(jié)合函數(shù)圖象,求b的取值范圍.
)經(jīng)過(1,-1),且與圖形W有公共點,結(jié)合函數(shù)圖象,求b的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
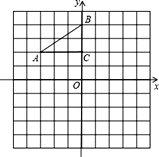
【題目】如圖,在平面直角坐標系中,Rt△ABC的三個頂點分別是A(﹣3,2),B(0,4),C(0,2).
(1)將△ABC以點C為旋轉(zhuǎn)中心旋轉(zhuǎn)180°,畫出旋轉(zhuǎn)后對應(yīng)的△A1B1C1,平移△ABC,若點A的對應(yīng)點A2的坐標為(0,﹣4),畫出平移后對應(yīng)的△A2B2C2;
(2)若將△A1B1C1繞某一點旋轉(zhuǎn)可以得到△A2B2C2,請直接寫出旋轉(zhuǎn)中心的坐標.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
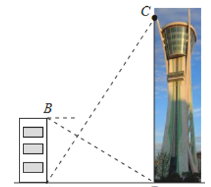
【題目】為測量觀光塔高度,如圖,一人先在附近一樓房的底端A點處觀測觀光塔頂端C處的仰角是60°,然后爬到該樓房頂端B點處觀測觀光塔底部D處的俯角是30°.已知樓房高AB約是45m,請根據(jù)以上觀測數(shù)據(jù)求觀光塔的高.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com