
【題目】如圖,雙曲線![]() 經過點
經過點![]() 與點
與點![]() ,則
,則![]() 的面積為( )
的面積為( )

A. 2 B. 3 C. 4 D. 5
【答案】B
【解析】
過A、B分別作x軸的垂線,垂足分別為C、D,把點A(2,2)代入雙曲線y=![]() 確定k的值,再把點B(4,m)代入雙曲線y=
確定k的值,再把點B(4,m)代入雙曲線y=![]() ,確定點B的坐標,根據S△AOB=S△AOC+S梯形ABDCS△BOD和三角形的面積公式與梯形的面積公式進行計算即可.
,確定點B的坐標,根據S△AOB=S△AOC+S梯形ABDCS△BOD和三角形的面積公式與梯形的面積公式進行計算即可.
過A、B分別作x軸的垂線,垂足分別為C、D,如圖,

∵雙曲線y=![]() 經過點A(2,2),
經過點A(2,2),
∴k=2×2=4,
而點B(4,m)在y=![]() 上,
上,
∴4m=4,解得m=1,
即B點坐標為(4,1),
∴S△AOB=S△AOC+S梯形ABDCS△BOD=![]() OCAC+
OCAC+![]() ×(AC+BD)×CD
×(AC+BD)×CD![]() ×OD×BD=
×OD×BD=![]() ×2×2+
×2×2+![]() ×(2+1)×(42)
×(2+1)×(42)![]() ×4×1=3.
×4×1=3.
故選:B.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:初中數學 來源: 題型:
【題目】隨著人民生活水平不斷提高,我市“初中生帶手機”現象也越來越多,為了了解家長對此現象的態度,某校數學課外活動小組隨機調查了若干名學生家長,并將調查結果進行統計,得出如下所示的條形統計圖和扇形統計圖.

問:(1)這次調查的學生家長總人數為 .
(2)請補全條形統計圖,并求出持“很贊同”態度的學生家長占被調查總人數的百分比.
(3)求扇形統計圖中表示學生家長持“無所謂”態度的扇形圓心角的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,在菱形
,在菱形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 相交于點
相交于點![]() .
.
![]() 求邊
求邊![]() 的長;
的長;
![]() 如圖
如圖![]() ,將一個足夠大的直角三角板
,將一個足夠大的直角三角板![]() 角的頂點放在菱形
角的頂點放在菱形![]() 的頂點
的頂點![]() 處,繞點
處,繞點![]() 左右旋轉,其中三角板
左右旋轉,其中三角板![]() 角的兩邊分別與邊
角的兩邊分別與邊![]() ,
,![]() 相交于點
相交于點![]() ,
,![]() ,連接
,連接![]() 與
與![]() 相交于點
相交于點![]() .
.
①判斷![]() 是哪一種特殊三角形,并說明理由;
是哪一種特殊三角形,并說明理由;
②旋轉過程中,當點![]() 為邊
為邊![]() 的四等分點時
的四等分點時![]() ,求
,求![]() 的長.
的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個均勻的立方體骰子六個面上標有數1,2,3,4,5,6,若以連續擲兩次骰子得到的數![]() 作為點
作為點![]() 的坐標,則點
的坐標,則點![]() 落在反比例函數
落在反比例函數![]() 圖象與坐標軸所圍成區域內(含落在此反比例函數的圖象上的點)的概率是( )
圖象與坐標軸所圍成區域內(含落在此反比例函數的圖象上的點)的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校初三年級(1)班要舉行一場畢業聯歡會.規定每個同學分別轉動下圖中兩個可以自由轉動的均勻轉盤A、B(轉盤A被均勻分成三等份.每份分別標上1.2,3三個釹宇.轉盤B被均勻分成二等份.每份分別標上4,5兩個數字).若兩個轉盤停止后指針所指區域的數字都為偶數(如果指針恰好指在分格線上.那么重轉直到指針指向某一數字所在區域為止).則這個同學要表演唱歌節目.請求出這個同學表演唱歌節目的概率(要求用畫樹狀圖或列表方法求解)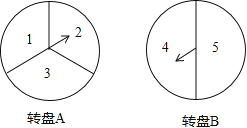
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在平面直角坐標系中,正比例函數![]() 圖像與反比例函數
圖像與反比例函數![]() 交于點A(4,
交于點A(4, ![]() ),過點A作
),過點A作![]() 的垂線交x軸于點B.
的垂線交x軸于點B.

(1)求反比例函數的解析式;
(2)如果點C在![]() 的圖像上,且△CAB的面積為△OAB面積的2倍,求點C的坐標.
的圖像上,且△CAB的面積為△OAB面積的2倍,求點C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:
若一個整數能表示成a2+b2(a、b是整數)的形式,則稱這個數為“平和數”,例如5是“平和數”,因為5=22+1,再如,M=x2+2xy+2y2=(x+y)2+y2(x, y是整數),我們稱M也是“平和數”.
(1)請你寫一個小于5的“平和數”,并判斷34是否為“平和數”.
(2)已知S=x2+9y2+6x﹣6y+k(x,y是整數,k是常數,要使S為“平和數”,試求出符合條件的一個k值,并說明理由.
(3)如果數m,n都是“平和數”,試說明![]() 也是“平和數”.
也是“平和數”.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在平行四邊形![]() 中,
中,![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 的中點,
的中點,![]() 分別交
分別交![]() 、
、![]() 于
于![]() 、
、![]() .請判斷下列結論:
.請判斷下列結論:![]() ;
;![]() ;
;![]() ;
;![]() .其中正確的結論有( )
.其中正確的結論有( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com