
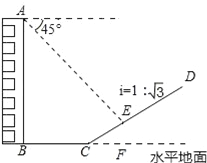
【題目】如圖,一樓房AB后有一假山,其坡度為i=1: ![]() ,山坡坡面上E點處有一休息亭,測得假山坡腳C與樓房水平距離BC=25米,與亭子距離CE=20米,小麗從樓房頂測得E點的俯角為45°,求樓房AB的高.(注:坡度i是指坡面的鉛直高度與水平寬度的比)
,山坡坡面上E點處有一休息亭,測得假山坡腳C與樓房水平距離BC=25米,與亭子距離CE=20米,小麗從樓房頂測得E點的俯角為45°,求樓房AB的高.(注:坡度i是指坡面的鉛直高度與水平寬度的比)
【答案】樓房AB的高為(35+10![]() )米.
)米.
【解析】試題分析:過點E作EF⊥BC的延長線于F,EH⊥AB于點H,根據CE=20米,坡度為i=1: ![]() ,分別求出EF、CF的長度,在Rt△AEH中求出AH,繼而可得樓房AB的高.
,分別求出EF、CF的長度,在Rt△AEH中求出AH,繼而可得樓房AB的高.
試題解析:過點E作EF⊥BC的延長線于F,EH⊥AB于點H,
在Rt△CEF中,
∵i=![]() =
=![]() =tan∠ECF,
=tan∠ECF,
∴∠ECF=30°,
∴EF=![]() CE=10米,CF=10
CE=10米,CF=10![]() 米,
米,
∴BH=EF=10米,HE=BF=BC+CF=(25+10![]() )米,
)米,
在Rt△AHE中,∵∠HAE=45°,
∴AH=HE=(25+10![]() )米,
)米,
∴AB=AH+HB=(35+10![]() )米.
)米.
答:樓房AB的高為(35+10![]() )米.
)米.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某年級組織學生參加夏令營,分為甲、乙、丙三組進行活動.下面兩幅統計圖反映了學生報名參加夏令營的情況.請你根據圖中的信息回答下列問題:![]()
![]()
報名人數分布直方圖 報名人數扇形統計圖
(1)求該年級報名參加本次活動的總人數;
(2)求該年級報名參加乙組的人數,并補全頻數分布直方圖;
(3)根據實際情況,需從甲組抽調部分同學到丙組,使丙組人數是甲組人數的3倍,那么,應從甲組抽調多少名學生到丙組?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】通過類比聯想、引申拓展研究典型題目,可達到解一題知一類的目的.下面是一個案例.
原題:如圖①,點 ![]() 分別在正方形
分別在正方形 ![]() 的邊
的邊 ![]() 上,
上, ![]() ,連接
,連接 ![]() ,則
,則 ![]() ,試說明理由.
,試說明理由.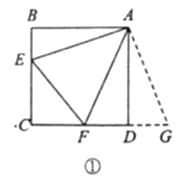
(1)思路梳理
因為 ![]() ,所以把
,所以把 ![]() 繞點
繞點 ![]() 逆時針旋轉90°至
逆時針旋轉90°至 ![]() ,可使
,可使 ![]() 與
與 ![]() 重合.因為
重合.因為 ![]() ,所以
,所以 ![]() ,點
,點 ![]() 共線.
共線.
根據 , 易證 ![]() , 得
, 得 ![]() .請證明.
.請證明.
(2)類比引申
如圖②,四邊形 ![]() 中,
中, ![]() ,
, ![]() ,點
,點 ![]() 分別在邊
分別在邊 ![]() 上,
上, ![]() .若
.若 ![]() 都不是直角,則當
都不是直角,則當 ![]() 與
與 ![]() 滿足等量關系時,
滿足等量關系時, ![]() 仍然成立,請證明.
仍然成立,請證明.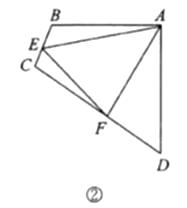
(3)聯想拓展
如圖③,在 ![]() 中,
中, ![]() ,點
,點 ![]() 均在邊
均在邊 ![]() 上,且
上,且 ![]() .猜想
.猜想 ![]() 應滿足的等量關系,并寫出證明過程.
應滿足的等量關系,并寫出證明過程.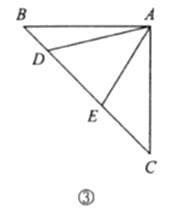
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2016年3月,我市某中學舉行了“愛我中國朗誦比賽”活動,根據學生的成績劃分為A、B、C、D四個等級,并繪制了不完整的兩種統計圖.根據圖中提供的信息,回答下列問題:
(1)參加朗誦比賽的學生共有 人,并把條形統計圖補充完整;
(2)扇形統計圖中,m= ,n= ;C等級對應扇形有圓心角為 度;
(3)學校欲從獲A等級的學生中隨機選取2人,參加市舉辦的朗誦比賽,請利用列表法或樹形圖法,求獲A等級的小明參加市朗誦比賽的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是等邊三角形,AD是角平分線,△ADE是等邊三角形,下列結論:①AD⊥BC;②EF=FD;③BE=BD.其中正確結論的個數為( )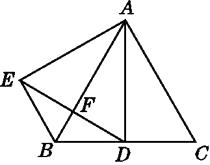
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一次新冠病毒防疫知識競賽有25道題,評委會決定:答對一道題得4分,答錯或不答一題扣1分,在這次知識競賽中,小明被評為優秀(85分或85分以上),那么小明至少答對了__________道題.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義符號min{a,b}的含義為:當a≥b時min{a,b}=b;當a<b時min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.則min{﹣x2+1,﹣x}的最大值是( )
A. ![]() B.
B. ![]() C. 1 D. 0
C. 1 D. 0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com