
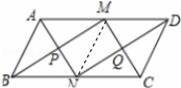
已知:如圖,M、N分別是▱ABCD的對邊中點,且AD=2AB,求證:PMQN為矩形.


【考點】矩形的判定;平行四邊形的性質.
【專題】證明題.
【分析】連接MN.由于四邊形ABCD是平行四邊形,那么AD平行且等于BC,而M、N是AD、BC的中點,從而可證DM平行且等于BN,于是可證四邊形BNDM是平行四邊形,則BM∥DN,同理可證AN∥CM,那么可證四邊形PNQM是平行四邊形,由于AM平行等于BN,且AB=BN=
 BC,則可知四邊形ABNM是菱形,利用菱形的性質,可知AN⊥BM,即∠MPN=90°,那么平行四邊形PNQM是矩形.
BC,則可知四邊形ABNM是菱形,利用菱形的性質,可知AN⊥BM,即∠MPN=90°,那么平行四邊形PNQM是矩形.
【解答】證明:連接MN,如圖所示:
∵ABCD為平行四邊形,
∴AD平行且等于BC,
又∵M為AD的中點,N為BC的中點,
∴MD平行且等于BN,
∴BNDM為平行四邊形,
∴BM∥ND,
同理AN∥MC,
∴四邊形PMQN為平行四邊形,
連接MN,
∵AM平行且等于BN,
∴四邊形ABNM為平行四邊形,
又∵AD=2AB,M為AD中點,
∴BN=AB,
∴四邊形ABNM為菱形,
∴AN⊥BM,
∴平行四邊形PMQN為矩形.

【點評】本題考查了平行四邊形的判定和性質、菱形的判定和性質、矩形的判定;熟練掌握平行四邊形的判定與性質,證出AN⊥BM是解決問題的關鍵.


 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:初中數學 來源: 題型:
為了解某校學生每日運動量,收集數據正確的是( )
A.調查該校七年級學生每日運動量;
B.調查該校女生每日的運動量
C.調查該校男生每日的運動量;
D.從七、八、九年級各抽調100人調查他們每日的運動量
查看答案和解析>>
科目:初中數學 來源: 題型:
為了研究某的高度h(千米)與溫度t(℃)之間的關系,某日研究人員在該地的不同高度處同時進行了若干次實驗,測得的數據如下表:
| h/千米 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
| t/℃ | 23 | 21 | 19 | 17 | 15 | 13 | 11 | … |
(1)在直角坐標系中,作出各組有序數對(h,t)所對應的點.
(2)這些點是否近似在一條直線上?
(3)估計此時3.5千米高度處的溫度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com