
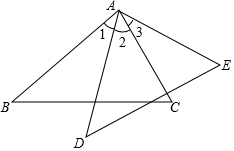
 如圖,∠1=∠3,∠B=∠D,AB=DE=5,BC=4,
如圖,∠1=∠3,∠B=∠D,AB=DE=5,BC=4,分析 (1)由∠1=∠3,推出∠1+∠2=∠3+∠2,即∠BAC=∠DAE,由∠B=∠D,即可根據兩角對應相等的兩個三角形相似進行證明.
(2)利用相似三角形的性質即可解決問題.
解答 (1)證明:∵∠1=∠3,
∴∠1+∠2=∠3+∠2,
即∠BAC=∠DAE,∵∠B=∠D,
∴△BAC∽△DAE.
(2)∵△BAC∽△DAE,
∴$\frac{AB}{AD}$=$\frac{CB}{DE}$,
∵AB=DE=5,BC=4,
∴$\frac{5}{AD}$=$\frac{4}{5}$,
∴AD=$\frac{25}{4}$.
點評 本題考查相似三角形的判定和性質,等式的性質等知識,解題的關鍵是熟練掌握相似三角形的判定和性質,屬于基礎題,中考常考題型.


科目:初中數學 來源: 題型:選擇題
| A. | 200(1+m%)2=148 | B. | 200(1-m%)2=148 | C. | 200(1-2m%)2=148 | D. | 200[1-(m%)2]=148 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
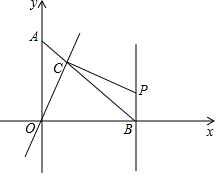 如圖,點A(0,a ),點B( b,0 )且滿足a2+2b2-2ab-2b+1=0.經過原點O的直線l交線段AB于點C,過C作OC⊥CP,與直線BP相交于點P,BP⊥OB.現將直線l繞O點旋轉,使交點C從A向B運動,但P點必須在第一象限內,分析此圖后,對下列問題作出探究:
如圖,點A(0,a ),點B( b,0 )且滿足a2+2b2-2ab-2b+1=0.經過原點O的直線l交線段AB于點C,過C作OC⊥CP,與直線BP相交于點P,BP⊥OB.現將直線l繞O點旋轉,使交點C從A向B運動,但P點必須在第一象限內,分析此圖后,對下列問題作出探究:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 絕對值相等的數 | |
| B. | 符號不同的數,其中正數的絕對值較大 | |
| C. | 符號不同的數,其中負數的絕對值較大 | |
| D. | 以上都不正確 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,某中學準備在校園里利用圍墻的一段,再砌三面墻,圍成一個矩形花園ABCD(圍墻MN最長可利用25m),現在已備足可以砌50m長的墻的材料.
如圖,某中學準備在校園里利用圍墻的一段,再砌三面墻,圍成一個矩形花園ABCD(圍墻MN最長可利用25m),現在已備足可以砌50m長的墻的材料.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com