
 的圖象與矩形AOBC的邊AC、BC分別相交于點E、F,且點C坐標為(4,3),將△CEF沿EF對折后,C點恰好落在OB上.
的圖象與矩形AOBC的邊AC、BC分別相交于點E、F,且點C坐標為(4,3),將△CEF沿EF對折后,C點恰好落在OB上.
 ,3),F(xiàn)(4,
,3),F(xiàn)(4, ),
),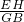 =
= ,
,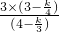 =
= ,
,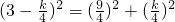 ,
, ;
;
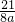 ),
),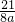 +3),
+3),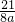 +3)=
+3)=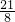 ,
,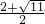 ,a=
,a=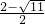 (舍去),
(舍去),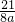 =
=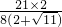 =
=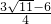 ,
,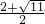 -2=
-2=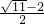 ,
,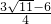 +3=
+3=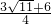 ,
,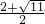 ,
,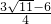 ),N(
),N(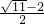 ,
,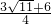 )
)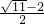 ,
,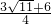 )N(
)N(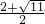 ,
,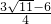 ).
).

 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案科目:初中數(shù)學 來源: 題型:
| k | x |
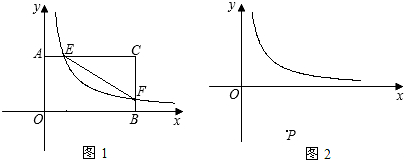
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
| 5 |
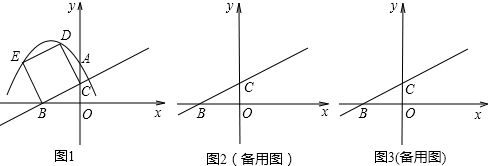
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
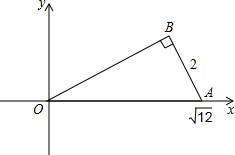 已知在Rt△OAB中,∠B=90°,AO=
已知在Rt△OAB中,∠B=90°,AO=| 12 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
| ||||
| a+12 |

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
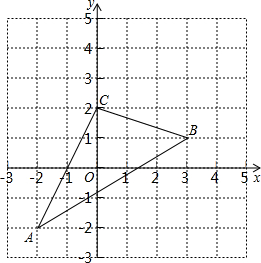 如圖,△ABC在直角坐標系中,
如圖,△ABC在直角坐標系中,查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com