
【題目】如圖,已知ABCD是邊長為3的正方形,點P在線段BC上,點G在線段AD上,PD=PG,DF⊥PG于點H,交AB于點F,將線段PG繞點P逆時針旋轉90°得到線段PE,連接EF.
(1)求證:DF=PG;
(2)若PC=1,求四邊形PEFD的面積.
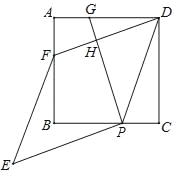
【答案】(1)證明見解析;(2)8.
【解析】
作PM⊥AD,在四邊形ABCD和四邊形ABPM證AD=PM;DF⊥PG,得出∠GDH+∠DGH=90°,推出∠ADF=∠MPG;還有兩個直角即可證明△ADF≌△MPG,從而得出對應邊相等
(2)由已知得,DG=2PC=2;△ADF≌△MPG得出DF=PD;根據旋轉,得出∠EPG=90°,PE=PG從而得出四邊形PEFD為平行四邊形;根據勾股定理和等量代換求出邊長DF的值;根據相似三角形得出對應邊成比例求出GH的值,從而求出高PH 的值;最后根據面積公式得出
解:(1)證明:∵四邊形ABCD為正方形,
∴AD=AB,
∵四邊形ABPM為矩形,
∴AB=PM,
∴AD=PM,
∵DF⊥PG,
∴∠DHG=90°,
∴∠GDH+∠DGH=90°,
∵∠MGP+∠MPG=90°,
∴∠GDH=∠MPG,
在△ADF和△MPG中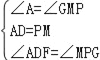 ,
,
∴△ADF≌△MPG(ASA),
∴DF=PG;
(2)作PM⊥DG于M,如圖,
∵PD=PG,
∴MG=MD,
∵四邊形ABCD為矩形,
∴PCDM為矩形,
∴PC=MD,
∴DG=2PC=2;
∵△ADF≌△MPG(ASA),
∴DF=PG,
而PD=PG,
∴DF=PD,
∵線段PG繞點P逆時針旋轉90°得到線段PE,
∴∠EPG=90°,PE=PG,
∴PE=PD=DF,
而DF⊥PG,
∴DF∥PE,
即DF∥PE,且DF=PE,
∴四邊形PEFD為平行四邊形,
在Rt△PCD中,PC=1,CD=3,
∴PD=![]() =
=![]() ,
,
∴DF=PG=PD=![]() ,
,
∵四邊形CDMP是矩形,
∴PM=CD=3,MD=PC=1,
∵PD=PG,PM⊥AD,
∴MG=MD=1,DG=2,
∵∠GDH=∠MPG,∠DHG=∠PMG=90°,
∴△DHG∽△PMG,
∴![]() ,
,
∴GH=![]() =
=![]() ,
,
∴PH=PG﹣GH=![]() ﹣
﹣![]() =
=![]() ,
,
∴四邊形PEFD的面積=DFPH=![]() ×
×![]() =8.
=8.


科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,AD是邊BC上的中線,過點A作AE∥BC,過點D作DE∥AB,DE與AC、AE分別交于點O、點E,聯結EC.
(1)求證:四邊形ADCE是平行四邊形;
(2)當∠BAC=90°時,求證:四邊形ADCE是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的盒子里裝有只有顏色不同的黑、白兩種球共50個,小穎做摸球實驗,她將盒子里面的球攪勻后從中隨機摸出一個球記下顏色,再把它放回盒子中,不斷重復上述過程,下表是試驗中的一組統計數據:
摸到球的次數 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次數 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的概率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)請估計當![]() 很大時,摸到白球的頻率將會接近______;(精確到0.1);
很大時,摸到白球的頻率將會接近______;(精確到0.1);
(2)假如隨機摸一次,摸到白球的概率P(白球)=______;
(3)試估算盒子里白色的球有多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC 中,點 D 是邊 BC 上的點(與 B、C 兩點不重合),過點 D作 DE∥AC,DF∥AB,分別交 AB、AC 于 E、F 兩點,下列說法正確的是( )

A. 若 AD 平分∠BAC,則四邊形 AEDF 是菱形
B. 若 BD=CD,則四邊形 AEDF 是菱形
C. 若 AD 垂直平分 BC,則四邊形 AEDF 是矩形
D. 若 AD⊥BC,則四邊形 AEDF 是矩形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),AB=CD,AD=BC,O為AC中點,過O點的直線分別與AD、BC相交于點M、N,那么∠1與∠2有什么關系?請說明理由;
若過O點的直線旋轉至圖(2)、(3)的情況,其余條件不變,那么圖(1)中的∠1與∠2的關系成立嗎?請說明理由.
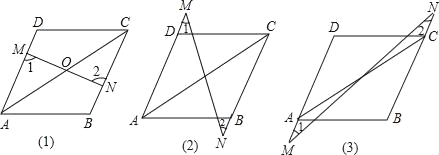
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,AB是直徑,CD是弦,AB⊥CD,垂足為E,連結CO,AD,∠BAD=20°,則下列說法中正確的是( )
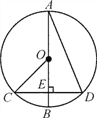
A. ∠BOC=2∠BAD B. CE=EO C. ∠OCE=40° D. AD=2OB
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com