
【題目】 ⑴如圖![]() ,在正方形
,在正方形![]() 中,點
中,點![]() 分別在
分別在![]() 上,
上,![]() 于點
于點![]() ,求證
,求證![]() ;
;
⑵如圖![]() ,將⑴中的正方形
,將⑴中的正方形![]() 改為矩形
改為矩形![]() ,
,![]()
![]() 于點
于點![]() ,探究
,探究![]() 與
與![]() 的數量關系,并證明你的結論.
的數量關系,并證明你的結論.

【答案】(1)見解析;(2)AB=![]() BC,見解析.
BC,見解析.
【解析】
試題分析:(1)根據正方形的性質,可得∠ABC與∠C的關系,AB與BC的關系,根據兩直線垂直,可得∠AMB的度數,根據直角三角形銳角的關系,可得∠ABM與∠BAM的關系,根據同角的余角相等,可得∠BAM與∠CBF的關系,根據ASA,可得△ABE≌△BCF,根據全等三角形的性質,可得答案;
(2)根據矩形的性質得到∠ABC=∠C,由余角的性質得到∠BAM=∠CBF,根據相似三角形的性質即可得到結論.
試題解析(1)證明:∵四邊形ABCD是正方形,∴∠ABC=∠C,AB=BC.
∵AE⊥BF,∴∠AMB=∠BAM+∠ABM=90°,
∵∠ABM+∠CBF=90°,∴∠BAM=∠CBF.
在△ABE和△BCF中,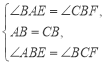 ,
,
∴△ABE≌△BCF(ASA),∴AE=BF;
(2)解:AB=![]() BC,
BC,
理由:∵四邊形ABCD是矩形,∴∠ABC=∠C,
∵AE⊥BF,∴∠AMB=∠BAM+∠ABM=90°,
∵∠ABM+∠CBF=90°,∴∠BAM=∠CBF,∴△ABE∽△BCF,
∴![]() ,∴AB=
,∴AB=![]() BC.
BC.


科目:初中數學 來源: 題型:
【題目】某中學女子足球隊15名隊員的年齡情況如下表:
年齡(歲) | 13 | 14 | 15 | 16 |
隊員(人) | 2 | 3 | 6 | 4 |
這支球隊隊員的年齡的眾數和中位數分別是( )
A.14,15
B.14,14.5
C.15,15
D.15,14
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班為滿足同學們課外活動的需求,要求購排球和足球若干個.已知足球的單價比排球的單價多![]() 元,用
元,用![]() 元購得的排球數量與用
元購得的排球數量與用![]() 元購得的足球數量相等.
元購得的足球數量相等.
⑴排球和足球的單價各是多少元?
⑵若恰好用去![]() 元,有哪幾種購買方案?
元,有哪幾種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 九⑴班![]() 名學生參加學校舉行的“珍惜生命,遠離毒品”只是競賽初賽,賽后,班長對成績進行分析,制作如下的頻數分布表和頻數分布直方圖(未完成).余下
名學生參加學校舉行的“珍惜生命,遠離毒品”只是競賽初賽,賽后,班長對成績進行分析,制作如下的頻數分布表和頻數分布直方圖(未完成).余下![]() 名學生成績尚未統計,這
名學生成績尚未統計,這![]() 名學生成績如下:
名學生成績如下:![]() .
.
頻數分布表
分數段 | 頻數(人數) |
|
|
|
|
|
|
|
|

請解答下列問題:
⑴完成頻數分布表,![]() ,
,![]() .
.
⑵補全頻數分布直方圖;
⑶全校共有![]() 名學生參加初賽,估計該校成績
名學生參加初賽,估計該校成績![]() 范圍內的學生有多少人?
范圍內的學生有多少人?
⑷九⑴班甲、乙、丙三位同學的成績并列第一,現選兩人參加決賽,求恰好選中甲、乙兩位同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分8分)
在四邊形ABCD中,對角線AC、BD交于點O.若四邊形ABCD是正方形如圖1:則有AC=BD,AC⊥BD.
旋轉圖1中的Rt△COD到圖2所示的位置,AC’與BD’有什么關系?(直接寫出)
若四邊形ABCD是菱形,∠ABC=60°,旋轉Rt△COD至圖3所示的位置,AC’與BD’又有什么關系?寫出結論并證明.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com