
【題目】如圖,某校有一塊長為(5a+b)米,寬為(3a+b)米的長方形空地,中間是邊長(a﹣b)米的正方形草坪,其余為活動場地,學校計劃將活動場地(陰影部分)進行硬化.
(1)用含a,b的代數式表示需要硬化的面積并化簡;
(2)當a=5,b=2時,求需要硬化的面積.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】一個不透明的袋中裝有5個黃球,13個黑球和22個紅球,它們除顏色外都相同.
(1)小明和小紅玩摸球游戲,規定每人摸球后再將摸到的球放回去為一次游戲.若摸到黑球小明獲勝,摸到黃球小紅獲勝,這個游戲對雙方公平嗎?請說明你的理由;
(2)現在裁判想從袋中取出若干個黑球,并放入相同數量的黃球,使得這個游戲對雙方公平,問取出了多少黑球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于一個三位正整數t,將各數位上的數字重新排序后(包括本身),得到一個新的三位數 ![]() (a≤c),在所有重新排列的三位數中,當|a+c﹣2b|最小時,稱此時的
(a≤c),在所有重新排列的三位數中,當|a+c﹣2b|最小時,稱此時的 ![]() 為t的“最優組合”,并規定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后為:142、214、因為|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124為124的“最優組合”,此時F(124)=﹣1.
為t的“最優組合”,并規定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后為:142、214、因為|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124為124的“最優組合”,此時F(124)=﹣1.
(1)三位正整數t中,有一個數位上的數字是另外兩數位上的數字的平均數,求證:F(t)=0
(2)一個正整數,由N個數字組成,若從左向右它的第一位數能被1整除,它的前兩位數能被2整除,前三位數能被3整除,…,一直到前N位數能被N整除,我們稱這樣的數為“善雅數”.例如:123的第一位數1能披1整除,它的前兩位數12能被2整除,前三位數123能被3整除,則123是一個“善雅數”.若三位“善雅數”m=200+10x+y(0≤x≤9,0≤y≤9,x、y為整數),m的各位數字之和為一個完全平方數,求出所有符合條件的“善雅數”中F(m)的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
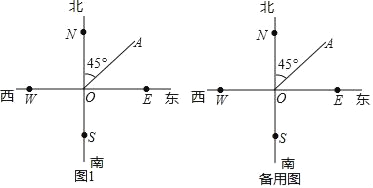
【題目】如圖,射線ON、OE、OS、OW分別表示從點O出發北、東、南、西四個方向,點A在點O的北偏東45°方向,點B在點O的北偏西30°方向.
(1)畫出射線OB,若∠BOC與∠AOB互余,請在圖1或備用圖中畫出∠BOC;
(2)若OP是∠AOC的角平分線,直接寫出∠AOP的度數(不需要計算過程).
查看答案和解析>>
科目:初中數學 來源: 題型:
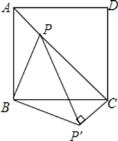
【題目】如圖所示,點P是正方形ABCD內的一點,連接AP,BP,CP,將△PAB繞著點B順時針旋轉90°到△P′CB的位置.若AP=2,BP=4,∠APB=135°,求PP′及PC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是我校某班同學隨機抽取的我國100座城市2017年某天當地pm2.5值的情況的條形統計圖,那么本次調查中,PM2.5值的中位數為微克/立方米.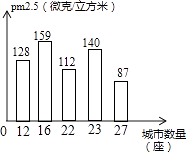
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24 ㎝,BC=26㎝,動點P從點A開始沿AD邊以每秒1㎝的速度向D點運動,動點Q從點C開始沿CB邊以每秒3㎝的速度向B運動,P,Q分別從A,C同時出發,當其中一點到達端點時,另一點也隨之停止運動,設運動時間為t s.
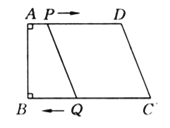
(1)t為何值時,四邊形PQCD為平行四邊形?
(2)t為何值時,四邊形PQCD為等腰梯形?
(3)t為何值時,四邊形ABQP為矩形?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com