
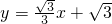 與x軸、y軸分別交于A、B兩點,⊙M經過
與x軸、y軸分別交于A、B兩點,⊙M經過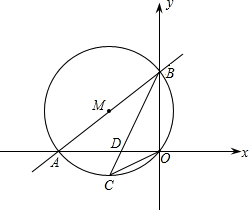 原點O及A、B兩點.
原點O及A、B兩點.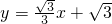 與x軸、y軸分別交于A、B兩點,
與x軸、y軸分別交于A、B兩點, )
) .
. +3)x+3
+3)x+3 =0.
=0.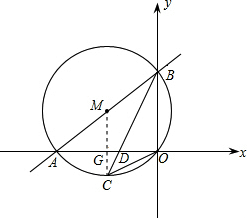
 OA=
OA= .
.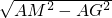 =
= ,
, AB=
AB=
 =
=
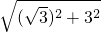 =
=
 -
- =
= .
. ,-
,- ).
).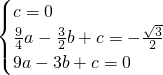 ,
,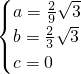 ,
,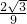 x2+
x2+ x.
x.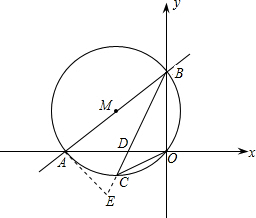
 ,OA=3;
,OA=3; ,
, ∠ABO,
∠ABO, ×
× =1.
=1.

 名師導航單元期末沖刺100分系列答案
名師導航單元期末沖刺100分系列答案 名校名卷單元同步訓練測試題系列答案
名校名卷單元同步訓練測試題系列答案科目:初中數學 來源:2010-2011學年浙江省杭州市蕭山區朝暉中學九年級(上)數學階段性測試卷(全冊)(解析版) 題型:填空題
 與雙曲線
與雙曲線 (k>0)交于A、B兩點,點A、B的橫坐標之比為1:3,則k= .
(k>0)交于A、B兩點,點A、B的橫坐標之比為1:3,則k= .
查看答案和解析>>
科目:初中數學 來源:2002年全國中考數學試題匯編《二次函數》(05)(解析版) 題型:解答題
 與x軸、y軸分別交于A、B兩點,⊙M經過原點O及A、B兩點.
與x軸、y軸分別交于A、B兩點,⊙M經過原點O及A、B兩點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com