
【題目】計算
(1)![]()
(2)![]()
(3)0-(-5)
(4)-2.5-5.9
(5)12-(-18)+(-7)-15
(6)![]()
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
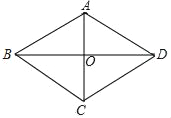
【題目】如圖所示,已知平行四邊形ABCD,對角線AC,BD相交于點O,∠BAO=∠DAO.
(1)求證:平行四邊形ABCD是菱形;
(2)請添加一個條件使菱形ABCD為正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,以
,以![]() 為邊長作等邊
為邊長作等邊![]() ,過點
,過點![]() 作
作![]() 平行于
平行于![]() 軸,交直線
軸,交直線![]() 于點
于點![]() ,以
,以![]() 為邊長作等邊
為邊長作等邊![]() ,過點
,過點![]() 作
作![]() 平行于
平行于![]() 軸,交直線
軸,交直線![]() 于點
于點![]() ,以
,以![]() 為邊長作等邊
為邊長作等邊![]() ,…,則等邊
,…,則等邊![]() 的邊長是______.
的邊長是______.

查看答案和解析>>
科目:初中數學 來源: 題型:
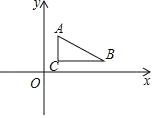
【題目】已知,如圖,A點坐標是(1,3),B點坐標是(5,1),C點坐標是(1,1)
(1)求△ABC的面積是____;
(2)求直線AB的表達式;
(3)一次函數y=kx+2與線段AB有公共點,求k的取值范圍;
(4)y軸上有一點P且△ABP與△ABC面積相等,則P點坐標是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于一元二次方程![]() ,下列說法:①若a+c=0,方程
,下列說法:①若a+c=0,方程![]() 有兩個不等的實數根;②若方程
有兩個不等的實數根;②若方程![]() 有兩個不等的實數根,則方程
有兩個不等的實數根,則方程![]() 也一定有兩個不等的實數根;③若c是方程
也一定有兩個不等的實數根;③若c是方程![]() 的一個根,則一定有
的一個根,則一定有![]() 成立;④若m是方程
成立;④若m是方程![]() 的一個根,則一定有
的一個根,則一定有![]() 成立.其中正確地只有 ( )
成立.其中正確地只有 ( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中數學 來源: 題型:
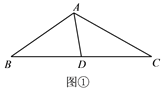
【題目】問題情境
小明和小麗共同探究一道數學題:
如圖①,在△ABC中,點D是邊BC的中點,∠BAD=65°,∠DAC=50°,AD=2,
求AC.
探索發現
小明的思路是:延長AD至點E,使DE=AD,構造全等三角形.
小麗的思路是:過點C作CE∥AB,交AD的延長線于點E,構造全等三角形.
選擇小明、小麗其中一人的方法解決問題情境中的問題.
類比應用
如圖②,在四邊形ABCD中,對角線AC、BD相交于點O,點O是BD的中點,
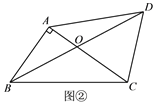
AB⊥AC.若∠CAD=45°,∠ADC=67.5°,AO=2,則BC的長為___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某檢修小組從A地出發,在東西向的馬路上檢修線路,如果規定向東行駛為正,向西行駛為負,一天中七次行駛紀錄如下.(單位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)求收工時,檢修小組在![]() 地的何方向?距離
地的何方向?距離![]() 地多遠?
地多遠?
(2)在第幾次紀錄時距![]() 地最遠?
地最遠?
(3)若汽車行駛每千米耗油0.4升,問從![]() 地出發,檢修結束后再回到
地出發,檢修結束后再回到![]() 地共耗油多少升?
地共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】感知:如圖(1),已知正方形ABCD和等腰直角△EBF,點E在正方形BC邊上,點F在AB邊的延長線上,∠EBF=90°,連結AE、CF.
易證:∠AEB=∠CFB(不需要證明).
探究:如圖(2),已知正方形ABCD和等腰直角△EBF,點E在正方形ABCD內部,點F在正方形ABCD外部,∠EBF=90°,連結AE、CF.
求證:∠AEB=∠CFB
應用:如圖(3),在(2)的條件下,當A、E、F三點共線時,連結CE,若AE=1,EF=2,則CE=______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近年來,我國很多地區持續出現霧霾天氣.某社區為了調查本社區居民對霧霾天氣主要成因的認識情況,隨機對該社區部分居民進行了問卷調查,要求居民從五個主要成因中只選擇其中的一項,被調查居民都按要求填寫了問卷.社區對調查結果進行了整理,繪制了如下不完整的統計圖表.被調查居民選擇各選項人數統計表
霧霾天氣的主要成因 | 頻數(人數) |
A大氣氣壓低,空氣不流動 | m |
B地面灰塵大,空氣濕度低 | 40 |
C汽車尾氣排放 | n |
D工廠造成的污染 | 120 |
E其他 | 60 |
請根據圖表中提供的信息解答下列問題:

(1)填空:m=________,n=________,扇形統計圖中C選項所占的百分比為________.
(2)若該社區居民約有6 000人,請估計其中會選擇D選項的居民人數.
(3)對于“霧霾”這個環境問題,請你用簡短的語言發出倡議.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com