
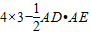
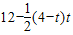
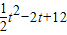 (0≤t≤3)
(0≤t≤3)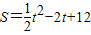
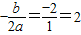
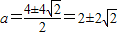 ,
,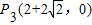
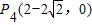 ,
,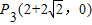 ,
,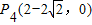 ,P5(0,4),P6(0,2).
,P5(0,4),P6(0,2).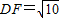 ,
,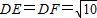 ,
,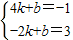 ,
,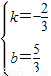 ,
, x+
x+ .(10分)
.(10分) ,0),N(0,
,0),N(0, ).(12分)
).(12分)

科目:初中數學 來源: 題型:
 A點運動,E為AB上一動點,點E以1cm/s的速度從A點出發向點B運動.
A點運動,E為AB上一動點,點E以1cm/s的速度從A點出發向點B運動.查看答案和解析>>
科目:初中數學 來源: 題型:
 10、如圖,以矩形OABC的頂點O為原點,OA所在的直線為x軸,OC所在的直線為y軸,建立平面直角坐標系、已知OA=3,OC=2,點E是AB的中點,在OA上取一點D,將△BDA沿BD翻折,使點A落在BC邊上的點F處,若在y軸上存在點P,且滿足FE=FP,則P點坐標為
10、如圖,以矩形OABC的頂點O為原點,OA所在的直線為x軸,OC所在的直線為y軸,建立平面直角坐標系、已知OA=3,OC=2,點E是AB的中點,在OA上取一點D,將△BDA沿BD翻折,使點A落在BC邊上的點F處,若在y軸上存在點P,且滿足FE=FP,則P點坐標為查看答案和解析>>
科目:初中數學 來源: 題型:
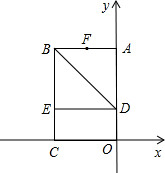 直角坐標系.已知OA=6,OC=4,在OA上取一點D,將△BDA沿BD翻折,點A恰好落在BC邊上的點E處.
直角坐標系.已知OA=6,OC=4,在OA上取一點D,將△BDA沿BD翻折,點A恰好落在BC邊上的點E處.查看答案和解析>>
科目:初中數學 來源: 題型:
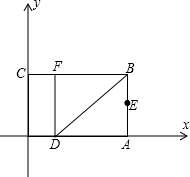 系.已知OA=3,OC=2,點E是AB的中點,在OA上取一點D,將△BDA沿BD翻折,使點A落在BC邊上的點F處.
系.已知OA=3,OC=2,點E是AB的中點,在OA上取一點D,將△BDA沿BD翻折,使點A落在BC邊上的點F處.查看答案和解析>>
科目:初中數學 來源: 題型:
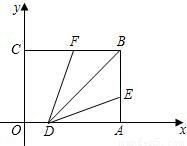
 如圖,以矩形OABC的頂點O為原點,OA所在的直線為x軸,OC所在的直線為y軸,建立平面直角坐標系.已知OA=3,OC=2,點E是AB的中點,在OA上取一點D,將△BDA沿BD翻折,使點A落在BC邊上的點F處.
如圖,以矩形OABC的頂點O為原點,OA所在的直線為x軸,OC所在的直線為y軸,建立平面直角坐標系.已知OA=3,OC=2,點E是AB的中點,在OA上取一點D,將△BDA沿BD翻折,使點A落在BC邊上的點F處.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com