
【題目】我們知道平行四邊形有很多性質.
現在如果我們把平行四邊形沿著它的一條對角線翻折,會發現這其中還有更多的結論.
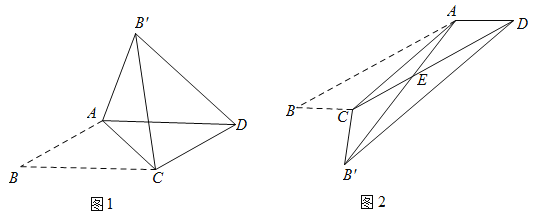
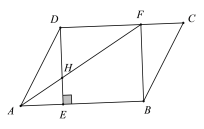
(發現與證明)![]() ABCD中,AB≠BC,將△ABC沿AC翻折至△AB′C,連結B′D.
ABCD中,AB≠BC,將△ABC沿AC翻折至△AB′C,連結B′D.
結論1:B′D∥AC;
結論2:△AB′C與![]() ABCD重疊部分的圖形是等腰三角形.
ABCD重疊部分的圖形是等腰三角形.
……
請利用圖1證明結論1或結論2(只需證明一個結論).
(應用與探究)在![]() ABCD中,已知∠B=30°,將△ABC沿AC翻折至△AB′C,連結B′D.
ABCD中,已知∠B=30°,將△ABC沿AC翻折至△AB′C,連結B′D.
(1)如圖1,若![]() ,則∠ACB= °,BC= ;
,則∠ACB= °,BC= ;
(2)如圖2,![]() ,BC=1,AB′與邊CD相交于點E,求△AEC的面積;
,BC=1,AB′與邊CD相交于點E,求△AEC的面積;
(3)已知![]() ,當BC長為多少時,是△AB′D直角三角形?
,當BC長為多少時,是△AB′D直角三角形?
【答案】【發現與證明】證明見解析;【應用與探究】(1) 45,![]() ;(2)
;(2)![]() ;(3)6,2, 4或3.
;(3)6,2, 4或3.
【解析】
試題【發現與證明】根據翻折對稱的性質,平行四邊形的性質和三角形內角和定理可得證.
【應用與探究】(1)∵△ABC沿AC翻折至△AB′C,∠B=30°,∴∠AB′C=∠B=30°.
∵![]() ,∴∠CB′D=45°.
,∴∠CB′D=45°.
由【發現與證明】的結論,B′D∥AC,
∴∠ACB=∠ACB′=∠C B′D=45°.
如答圖7,過A點作AP⊥BC于點P,
∵∠B=30°,![]() ,
,
∴![]() .
.
∵∠ACB=45°,∴![]() .
.
∴![]() .
.

(2)過C點分別作CG⊥AB,CH⊥A B′,垂足分別為G、H,應用含30度直角三角形的性質和勾股定理AE和CH的長即可求出△AEC的面積.
(3)分∠B′AD="90°," ∠AB′D=90°和∠ADB′=90°三種情況討論即可.
試題解析:解:【發現與證明】證明:如答圖1,設AD與B′C相交于點F,
∵△ABC沿AC翻折至△AB′C,
∴△ABC≌△△AB′C,∠ACB=∠ACB′,BC= B′C.
∵四邊形ABCD是平行四邊形,
∴AD=BC,AD∥BC.
∴B′C=AD,∠ACB=∠CAD.
∴![]() .∴AF=CF.
.∴AF=CF.
∴B′F=DF.
∴![]() .
.
∵∠AFC=∠B′FD,∴![]() .∴B′D∥AC.
.∴B′D∥AC.

【應用與探究】
(1)45,![]() .
.
(2)如答圖2,過C點分別作CG⊥AB,CH⊥AB′,垂足分別為G、H.
∴CG=CH.
在Rt△BCG中,∠BGC=90°,BC=1,∠B=30°,
∴![]() .
.
∵![]() ,∴.
,∴. ![]()
∵△AGC≌△AHC,∴![]() .
.
設AE=CE=x,
由勾股定理得,![]() ,即
,即 ,解得
,解得![]() .
.
∴△AEC的面積![]() .
.

(3)按△AB′D中的直角分類:
①當∠B′AD=90°時,如答圖3,
∵∠B′DA=∠DAC=∠B=30°,AB′=![]() ,∴BC=AD=6.
,∴BC=AD=6.
如答圖4,
∵∠A B′D=∠B=30°,AB′=![]() ,∴BC=AD=2.
,∴BC=AD=2.
②當∠AB′D=90°時,如答圖5,
∵∠B′AD=∠B=30°,AB′=![]() ,∴BC=AD=4.
,∴BC=AD=4.
③當∠ADB′=90°時,如答圖6,
∵∠DAB′=∠A B′C=∠B=30°,AB′=![]() ,∴BC=AD=3.
,∴BC=AD=3.
綜上所述, 當BC長為6,2, 4或3時,是△AB′D直角三角形.



科目:初中數學 來源: 題型:
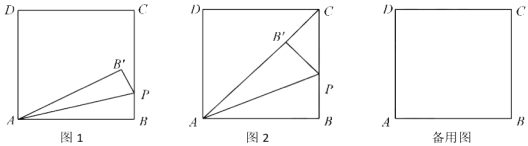
【題目】如圖1,在矩形![]() 中,BC=3,動點
中,BC=3,動點![]() 從
從![]() 出發,以每秒1個單位的速度,沿射線
出發,以每秒1個單位的速度,沿射線![]() 方向移動,作
方向移動,作![]() 關于直線
關于直線![]() 的對稱
的對稱![]() ,設點
,設點![]() 的運動時間為
的運動時間為![]()
(1)若![]()
①如圖2,當點B’落在AC上時,顯然△PCB’是直角三角形,求此時t的值
②是否存在異于圖2的時刻,使得△PCB’是直角三角形?若存在,請直接寫出所有符合題意的t的值?若不存在,請說明理由
(2)當P點不與C點重合時,若直線PB’與直線CD相交于點M,且當t<3時存在某一時刻有結論∠PAM=45°成立,試探究:對于t>3的任意時刻,結論∠PAM=45°是否總是成立?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 為坐標原點,以
為坐標原點,以![]() 所在的直線為
所在的直線為![]() 軸建立平面直角坐標系,如圖.按以下步驟作圖:①分別以點
軸建立平面直角坐標系,如圖.按以下步驟作圖:①分別以點![]() ,
,![]() 為圓心,以大于
為圓心,以大于![]() 的長為半徑作弧,兩弧相交于點
的長為半徑作弧,兩弧相交于點![]() ,
,![]() ;②作直線
;②作直線![]() 交
交![]() 于點
于點![]() .則點
.則點![]() 的坐標為( )
的坐標為( )
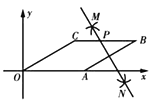
A.![]() B.
B.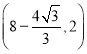 C.
C.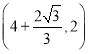 D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
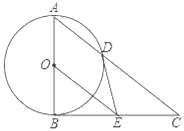
【題目】如圖,AB為⊙O直徑,BC為⊙O切線,連接A、C兩點,交⊙O于點D,BE=CE,連接DE,OE.
(1)判斷DE與⊙O的位置關系,并說明理由;
(2)求證:BC2=CD2OE;
(3)若cos∠BAD=![]() ,BE=6,求OE的長.
,BE=6,求OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(6分)某商場統計了今年1~5月A,B兩種品牌冰箱的銷售情況,并將獲得的數據繪制成折線統計圖.
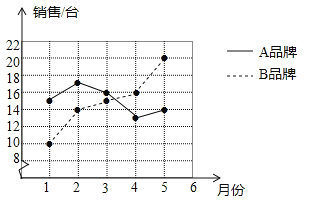
(1)分別求該商場這段時間內A,B兩種品牌冰箱月銷售量的中位數和方差;
(2)根據計算結果,比較該商場1~5月這兩種品牌冰箱月銷售量的穩定性.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,D、E分別是斜邊AB、直角邊BC上的點,把
,D、E分別是斜邊AB、直角邊BC上的點,把![]() 沿著直線DE折疊.
沿著直線DE折疊.

![]() 如圖1,當折疊后點B和點A重合時,用直尺和圓規作出直線DE;
如圖1,當折疊后點B和點A重合時,用直尺和圓規作出直線DE;![]() 不寫作法和證明,保留作圖痕跡
不寫作法和證明,保留作圖痕跡![]()
![]() 如圖2,當折疊后點B落在AC邊上點P處,且四邊形PEBD是菱形時,求折痕DE的長.
如圖2,當折疊后點B落在AC邊上點P處,且四邊形PEBD是菱形時,求折痕DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
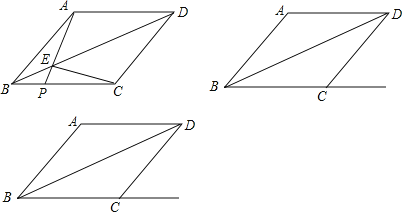
【題目】如圖,菱形ABCD中,AB=10,連接BD,點P是射線BC上一點(不與點B重合),AP與對角線BD交于點E,連接EC.
(1)求證:AE=CE;
(2)若sin∠ABD=![]() ,當點P在線段BC上時,若BP=4,求△PEC的面積;
,當點P在線段BC上時,若BP=4,求△PEC的面積;
(3)若∠ABC=45°,當點P在線段BC的延長線上時,請直接寫出△PEC是等腰三角形時BP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平行四邊形 ABCD 中,過點 D 作 DE⊥AB 于點 E,點 F 在 CD 上,CF =AE,連接 BF,AF.
(1)求證:四邊形 BFDE 是矩形;
(2)若 AF 平分∠BAD,交DE與H點,且 AB=3AE,BF=6,求AH的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com