
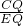 =2;
=2; ,∴PE=3+
,∴PE=3+ .
.
 EP=
EP= (3+
(3+ )=
)= +
+ ,
, +
+ )=
)= -
- x;
x; x;
x; (3+
(3+ )≤4,
)≤4,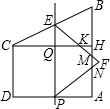
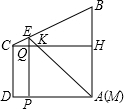
 ,∠HKM=∠HMK=45°;
,∠HKM=∠HMK=45°; =4-
=4- x;
x; x),即y=
x),即y= x-5;
x-5; ;
;
 x=4-
x=4- x,
x, x≤3,解得:
x≤3,解得: ≤x≤
≤x≤ ;
; ≤x≤
≤x≤ .
.

科目:初中數學 來源: 題型:
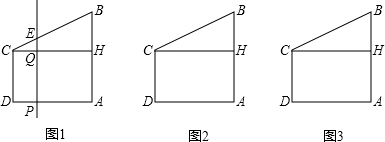
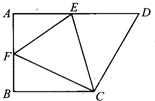 12、如圖,在直角梯形ABCD中,AD∥BC,∠B=90°,將直角梯形ABCD沿CE折疊,使點D落在AB上的F點,若AB=BC=12,EF=10,∠FCD=90°,則AF=
12、如圖,在直角梯形ABCD中,AD∥BC,∠B=90°,將直角梯形ABCD沿CE折疊,使點D落在AB上的F點,若AB=BC=12,EF=10,∠FCD=90°,則AF=查看答案和解析>>
科目:初中數學 來源: 題型:
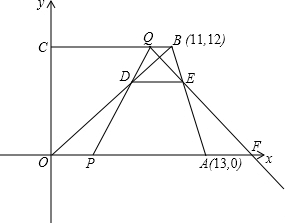 為t(單位:秒).
為t(單位:秒).查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•黑龍江)如圖,在直角梯形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于點E,在BC上截取BF=AE,連接AF交CE于點G,連接DG交AC于點H,過點A作AN⊥BC,垂足為N,AN交CE于點M.則下列結論;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正確的個數是( )
(2013•黑龍江)如圖,在直角梯形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于點E,在BC上截取BF=AE,連接AF交CE于點G,連接DG交AC于點H,過點A作AN⊥BC,垂足為N,AN交CE于點M.則下列結論;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正確的個數是( )查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=a,BC=b,AB=c,以AB為直徑作⊙O.試探究:
如圖,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=a,BC=b,AB=c,以AB為直徑作⊙O.試探究:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com