
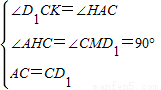 ,
,
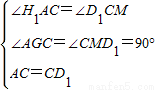 ,
,

科目:初中數(shù)學(xué) 來源: 題型:


查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:


查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2012年初中畢業(yè)升學(xué)考試(山東煙臺卷)數(shù)學(xué)(帶解析) 題型:解答題
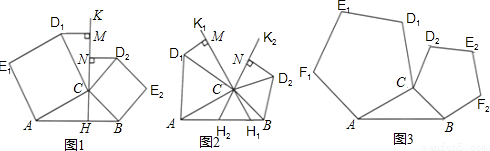
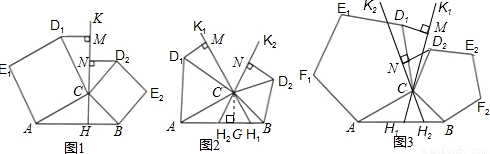
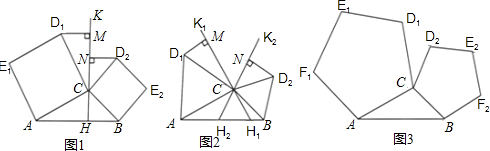
(1)問題探究
如圖1,分別以△ABC的邊AC與邊BC為邊,向△ABC外作正方形ACD1E1和正方形BCD2E2,過點C
作直線KH交直線AB于點H,使∠AHK=∠ACD1作D1M⊥KH,D2N⊥KH,垂足分別為點M,N.試探究線段D1M與線段D2N的數(shù)量關(guān)系,并加以證明.
(2)拓展延伸
①如圖2,若將“問題探究”中的正方形改為正三角形,過點C作直線K1H1,K2H2,分別交直線AB于點H1,H2,使∠AH1K1=∠BH2K2=∠ACD1.作D1M⊥K1H1,D2N⊥K2H2,垂足分別為點M,N.D1M=D2N是否仍成立?若成立,給出證明;若不成立,說明理由.
②如圖3,若將①中的“正三角形”改為“正五邊形”,其他條件不變.D1M=D2N是否仍成立?(要求:在
圖3中補(bǔ)全圖形,注明字母,直接寫出結(jié)論,不需證明)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2013年初中數(shù)學(xué)單元提優(yōu)測試卷-相似的判定解答題(帶解析) 題型:解答題
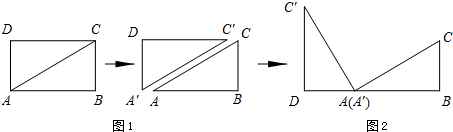
情境觀察將矩形ABCD紙片沿對角線AC剪開,得到△ABC和△A′C′D,如圖1所示.將△A′C′D的頂點A′與點A重合,并繞點A按逆時針方向旋轉(zhuǎn),使點D、A(A′)、B在同一條直線上,如圖2所示.
觀察圖2可知:與BC相等的線段是 _________ ,∠CAC′= _________ °.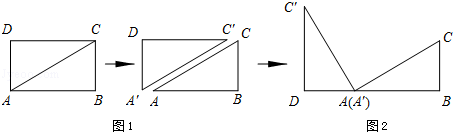
問題探究
如圖3,△ABC中,AG⊥BC于點G,以A為直角頂點,分別以AB、AC為直角邊,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,過點E、F作射線GA的垂線,垂足分別為P、Q.試探究EP與FQ之間的數(shù)量關(guān)系,并證明你的結(jié)論.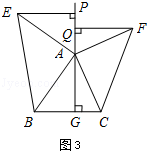
拓展延伸
如圖4,△ABC中,AG⊥BC于點G,分別以AB、AC為一邊向△ABC外作矩形ABME和矩形ACNF,射線GA交EF于點H.若AB=kAE,AC=kAF,試探究HE與HF之間的數(shù)量關(guān)系,并說明理由.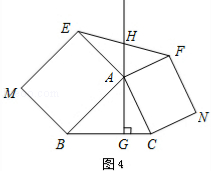
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com