
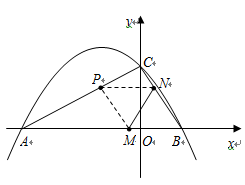
如圖,拋物線![]() 與
與![]() 軸交于A、B兩點(點A在點B左側(cè)),與y軸交
軸交于A、B兩點(點A在點B左側(cè)),與y軸交
于點C,且當(dāng)![]() =0和
=0和![]() =4時,y的值相等。直線y=4x-16與這條拋物線相交于兩點,其中一點的橫坐標(biāo)是3,另一點是這條拋物線的頂點M。
=4時,y的值相等。直線y=4x-16與這條拋物線相交于兩點,其中一點的橫坐標(biāo)是3,另一點是這條拋物線的頂點M。
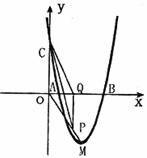
(1)求這條拋物線的解析式;
(2)P為線段OM上一點,過點P作PQ⊥![]() 軸于點Q。若點P在線段OM上運動(點P不與點O重合,但可以與點M重合),設(shè)OQ的長為t,四邊形PQCO的面積為S,求S與t之間的函數(shù)關(guān)系式及自變量t的取值范圍;
軸于點Q。若點P在線段OM上運動(點P不與點O重合,但可以與點M重合),設(shè)OQ的長為t,四邊形PQCO的面積為S,求S與t之間的函數(shù)關(guān)系式及自變量t的取值范圍;
(3)隨著點P的運動,四邊形PQCO的面積S有最大值嗎?如果S有最大值,請求出S的最大值并指出點Q的具體位置和四邊形PQCO的特殊形狀;如果S沒有最大值,請簡要說明理由;
(4)隨著點P的運動,是否存在t的某個值,能滿足PO=OC?如果存在,請求出t的值。
解:(1)∵當(dāng)![]() 和
和![]() 時,
時,![]() 的值相等,∴
的值相等,∴![]() ,
,
∴![]() ,∴
,∴![]()
將![]() 代入
代入![]() ,得
,得![]() ,
,
將![]() 代入
代入![]() ,得
,得![]()
∴設(shè)拋物線的解析式為![]()
將點![]() 代入,得
代入,得![]() ,解得
,解得![]() .
.
∴拋物線![]() ,即
,即![]()
(2)設(shè)直線OM的解析式為![]() ,將點M
,將點M![]() 代入,得
代入,得![]() ,
,
∴![]()
則點P![]() ,
,![]() ,而
,而![]() ,
,![]() .
.
![]() =
=![]()
![]() 的取值范圍為:
的取值范圍為:![]() <
<![]() ≤
≤![]()
(3)隨著點![]() 的運動,四邊形
的運動,四邊形![]() 的面積
的面積![]() 有最大值.
有最大值.
從圖像可看出,隨著點![]() 由
由![]() →
→![]() 運動,
運動,![]() 的面積與
的面積與![]() 的面積在不斷增大,即
的面積在不斷增大,即![]() 不斷變大,當(dāng)然點
不斷變大,當(dāng)然點![]() 運動到點
運動到點![]() 時,
時,![]() 最值
最值
此時![]() 時,點
時,點![]() 在線段
在線段![]() 的中點上
的中點上
因而![]() .
.
當(dāng)![]() 時,
時,![]() ,
,![]() ∥
∥![]() ,∴四邊形
,∴四邊形![]() 是平行四邊形.
是平行四邊形.
(4)隨著點![]() 的運動,存在
的運動,存在![]() ,能滿足
,能滿足![]()
設(shè)點![]() ,
,![]() ,
,![]() . 由勾股定理,得
. 由勾股定理,得![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() <
<![]() ,
,![]() (不合題意)
(不合題意)
∴當(dāng)![]() 時,
時,![]()


科目:初中數(shù)學(xué) 來源: 題型:
如圖,拋物線與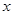 軸交于
軸交于![]() (
(![]() ,0)、
,0)、![]() (
(![]() ,0)兩點,且
,0)兩點,且![]() ,與
,與![]() 軸交于點
軸交于點![]() ,其中
,其中![]() 是方程
是方程![]() 的兩個根。(14分)
的兩個根。(14分)
(1)求拋物線的解析式;
 (2)點
(2)點![]() 是線段
是線段![]() 上的一個動點,過點
上的一個動點,過點![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,當(dāng)
,當(dāng)![]() 的面積最大時,求點
的面積最大時,求點![]() 的坐標(biāo);
的坐標(biāo);
(3)點![]() 在(1)中拋物線上,
在(1)中拋物線上,
點 為拋物線上一動點,在
為拋物線上一動點,在![]() 軸上是
軸上是
否存在點 ,使以
,使以![]() 為頂
為頂
點的四邊形是平行四邊形,如果存在,
求出所有滿足條件的點![]() 的坐標(biāo),
的坐標(biāo),
若不存在,請說明理由。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
如圖,拋物線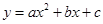 與
與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸相交于點
軸相交于點![]() .連結(jié)AC、BC,B、C兩點的坐標(biāo)分別為B(1,0)、
.連結(jié)AC、BC,B、C兩點的坐標(biāo)分別為B(1,0)、![]() ,且當(dāng)x=-10和x=8時函數(shù)的值
,且當(dāng)x=-10和x=8時函數(shù)的值![]() 相等.
相等.
1.求a、b、c的值;
2.若點![]() 同時從
同時從![]() 點出發(fā),均以每秒1個單位長度的速度分別沿
點出發(fā),均以每秒1個單位長度的速度分別沿![]() 邊運動,其中一個點到達終點時,另一點也隨之停止運動.連結(jié)
邊運動,其中一個點到達終點時,另一點也隨之停止運動.連結(jié)![]() ,將
,將![]() 沿
沿![]() 翻折,當(dāng)運動時間為幾秒時,
翻折,當(dāng)運動時間為幾秒時,![]() 點恰好落在
點恰好落在![]() 邊上的
邊上的![]() 處?并求點
處?并求點![]() 的坐標(biāo)及四邊形
的坐標(biāo)及四邊形![]() 的面積;
的面積;
3.上下平移該拋物線得到新的拋物線,設(shè)新拋物線的頂點為D,對稱軸與x軸的交點為E,若△ODE與△OBC相似,求新拋物線的解析式。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
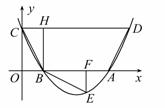
如圖,拋物線![]() 與
與![]() 軸交于A、B兩點,與
軸交于A、B兩點,與![]() 軸交于C點,四邊形OBHC為矩形,CH的延長
軸交于C點,四邊形OBHC為矩形,CH的延長![]() 線交拋物線于點D(5,2),連結(jié)BC、AD.
線交拋物線于點D(5,2),連結(jié)BC、AD.
(1)求C點的坐標(biāo)及拋物線的解析式;
(2)將△BCH繞點B按順時針旋轉(zhuǎn)90º后再沿![]() 軸對折得到△BEF(點C與點E對應(yīng)),判斷點E是否落在拋物線上,并說明理由;
軸對折得到△BEF(點C與點E對應(yīng)),判斷點E是否落在拋物線上,并說明理由;
(3)設(shè)過點E的直線交AB邊于點P,交CD邊于點Q. 問是否存在點P,使直線PQ分梯形ABCD的面積為1∶3兩部分?若存在,求出P點坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2013屆四川省鹽邊縣紅格中學(xué)九年級下學(xué)期摸底考試數(shù)學(xué)試卷(帶解析) 題型:解答題
如圖,拋物線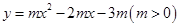 與
與 軸交于
軸交于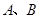 兩點,與
兩點,與 軸交于
軸交于 點.
點.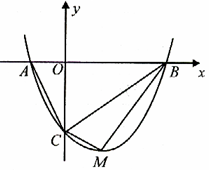
(1)請求出拋物線頂點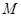 的坐標(biāo)(用含
的坐標(biāo)(用含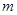 的代數(shù)式表示),
的代數(shù)式表示), 兩點的坐標(biāo);
兩點的坐標(biāo);
(2)經(jīng)探究可知, 與
與 的面積比不變,試求出這個比值;
的面積比不變,試求出這個比值;
(3)是否存在使 為直角三角形的拋物線?若存在,請求出;如果不存在,請說明理由.
為直角三角形的拋物線?若存在,請求出;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2012屆仙師中學(xué)九年級第一次月考試考試數(shù)學(xué)卷 題型:選擇題
如圖,拋物線與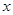 軸交于
軸交于 (
( ,0)、
,0)、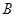 (
( ,0)兩點,且
,0)兩點,且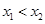 ,與
,與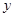 軸交于點
軸交于點 ,其中
,其中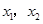 是方程
是方程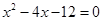 的兩個根。(14分)
的兩個根。(14分)
(1)求拋物線的解析式;
 (2)點
(2)點 是線段
是線段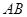 上的一個動點,過點
上的一個動點,過點 作
作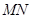 ∥
∥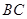 ,交
,交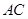 于點
于點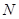 ,連接
,連接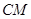 ,當(dāng)
,當(dāng)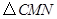 的面積最大時,求點
的面積最大時,求點 的坐標(biāo);
的坐標(biāo);
(3)點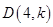 在(1)中拋物線上,
在(1)中拋物線上,
點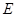 為拋物線上一動點,在
為拋物線上一動點,在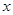 軸上是
軸上是
否存在點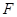 ,使以
,使以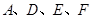 為頂
為頂
點的四邊形是平行四邊形,如果存在,
求出所有滿足條件的點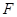 的坐標(biāo),
的坐標(biāo),
若不存在,請說明理由。
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com