
【題目】如圖,PB為⊙O的切線,B為切點,直線PO交⊙于點E、F,過點B作PO的垂線BA,垂足為點D,交⊙O于點A,延長AO與⊙O交于點C,連接BC,AF.
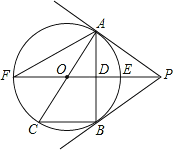
(1)求證:直線PA為⊙O的切線;
(2)試探究線段EF、OD、OP之間的等量關系,并加以證明;
(3)若BC=6,tan∠F=![]() ,求cos∠ACB的值和線段PE的長.
,求cos∠ACB的值和線段PE的長.
【答案】(1)證明見解析(2)EF2=4ODOP,證明見解析(3)![]() ,
,![]()
【解析】解:(1)連接OB,

∵PB是⊙O的切線,∴∠PBO=90°。
∵OA=OB,BA⊥PO于D,
∴AD=BD,∠POA=∠POB。
又∵PO=PO,∴△PAO≌△PBO(SAS)。
∴∠PAO=∠PBO=90°。∴直線PA為⊙O的切線。
(2)EF2=4ODOP。證明如下:
∵∠PAO=∠PDA=90°,∴∠OAD+∠AOD=90°,∠OPA+∠AOP=90°。
∴∠OAD=∠OPA。∴△OAD∽△OPA,∴![]() ,即OA2=ODOP。
,即OA2=ODOP。
又∵EF=2OA,∴EF2=4ODOP。
(3)∵OA=OC,AD=BD,BC=6,∴OD=![]() BC=3(三角形中位線定理)。
BC=3(三角形中位線定理)。
設AD=x,
∵tan∠F=![]() ,∴FD=2x,OA=OF=2x﹣3。
,∴FD=2x,OA=OF=2x﹣3。
在Rt△AOD中,由勾股定理,得(2x﹣3)2=x2+32,
解得,x1=4,x2=0(不合題意,舍去)。∴AD=4,OA=2x﹣3=5。
∵AC是⊙O直徑,∴∠ABC=90°。
又∵AC=2OA=10,BC=6,∴cos∠ACB=![]() 。
。
∵OA2=ODOP,∴3(PE+5)=25。∴PE=![]() 。
。
(1)連接OB,根據垂徑定理的知識,得出OA=OB,∠POA=∠POB,從而證明△PAO≌△PBO,然后利用全等三角形的性質結合切線的判定定理即可得出結論。
(2)先證明△OAD∽△OPA,由相似三角形的性質得出OA與OD、OP的關系,然后將EF=2OA代入關系式即可。
(3)根據題意可確定OD是△ABC的中位線,設AD=x,然后利用三角函數的知識表示出FD、OA,在Rt△AOD中,由勾股定理解出x的值,從而能求出cos∠ACB,再由(2)可得OA2=ODOP,代入數據即可得出PE的長。


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某大學生創業團隊抓住商機,購進一批干果分裝成營養搭配合理的小包裝后出售,每袋成本3元.試銷期間發現每天的銷售量y(袋)與銷售單價x(元)之間滿足一次函數關系,部分數據如表所示,其中3.5≤x≤5.5,另外每天還需支付其他費用80元.

(1)請直接寫出y與x之間的函數關系式;
(2)如果每天獲得160元的利潤,銷售單價為多少元?
(3)設每天的利潤為w元,當銷售單價定為多少元時,每天的利潤最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數 y=ax2+bx+c(a≠0)的圖象如圖,有下列 5 個結論:①4a+2b+c>0;②abc<0;③b<a+c;④3b>2c;⑤a+b<m(am+b),(m≠1 的實數);其中正確結論的個數為( )
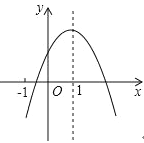
A. 2 個 B. 3 個 C. 4 個 D. 5 個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在三角形ABC中,BC=14,AC=9,AB=13,它的內切圓分別和BC、AC、AB切于點D、E、F,那么AF、BD、CE的長分別為( )
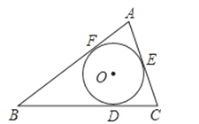
A. AF=4,BD=9,CE=5 B. AF=4,BD=5,CE=9
C. AF=5,BD=4,CE=9 D. AF=9,BD=4,CE=5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小明設計的“作平行四邊形ABCD的邊AB的中點”的尺規作圖過程.
已知:平行四邊形ABCD.
求作:點M,使點M 為邊AB 的中點.
作法:如圖,
①作射線DA;
②以點A 為圓心,BC長為半徑畫弧,
交DA的延長線于點E;
③連接EC 交AB于點M .
所以點M 就是所求作的點.

根據小明設計的尺規作圖過程,
(1)使用直尺和圓規,補全圖形 (保留作圖痕跡);
(2)完成下面的證明.
證明:連接AC,EB.
∵四邊形ABCD 是平行四邊形,
∴AE∥BC.
∵AE= ,
∴四邊形EBCA 是平行四邊形( )(填推理的依據) .
∴AM =MB ( )(填推理的依據) .
∴點M 為所求作的邊AB的中點.
查看答案和解析>>
科目:初中數學 來源: 題型:
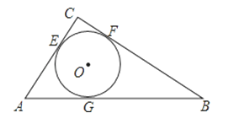
【題目】在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如圖,⊙O是△ABC的內切圓,與三邊分別相切于點E、F、G.
(1)求證:內切圓的半徑r=1;
(2)求tan∠OAG的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠A=∠B=90°,E是AB上的一點,且AE=BC,∠1=∠2.
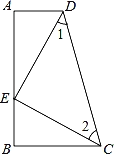
求證:△CED是等腰直角三角形
證明:∵∠1=∠2( )
∴EC= (在一個三角形中,等角對等邊)
∵∠A=∠B=90°,AE=BC
∴△AED≌△BCE( )
∴∠AED=∠ ( )
∵∠BCE+∠BEC=90°
∠ +∠BEC=90°(等量代換)
∴∠DEC=90°.
∴△CED是等腰直角三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB與x軸交于點C,與y軸交于點B,點A(1,3),點B(0,2).連接AO
(1)求直線AB的解析式;
(2)求三角形AOC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
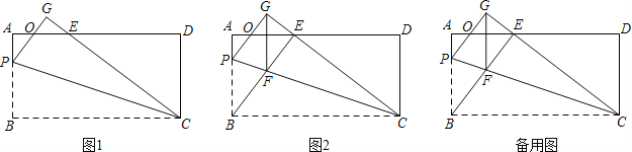
【題目】在矩形ABCD中,AB=12,BC=25,P是線段AB上一點(點P不與A,B重合),將△PBC沿直線PC折疊,頂點B的對應點是點G,CG,PG分別交線段AD于E,O.
(1)如圖1,若OP=OE,求證:AE=PB;
(2)如圖2,連接BE交PC于點F,若BE⊥CG.
①求證:四邊形BFGP是菱形;
②當AE=9,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com