如圖，在⊙O中，AB是直徑，AD是弦，∠ADE = 60°，∠C = 30°．
⑴判斷直線CD是否是⊙O的切線，并說明理由；
⑵若CD =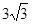 
，求BC的長．
（1）CD是⊙O的切線．
證明：如圖，連接OD．
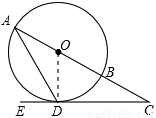
∵∠ADE=60°，∠C=30°，∴∠A=30°．
∵OA=OD，∴∠ODA=∠A=30°．
∴∠ODE=∠ODA+∠ADE=30°+60°=90°，∴OD⊥CD．
∴CD是⊙O的切線．
（2）解：在Rt△ODC中，∠ODC=90°， ∠C=30°，
CD=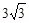
．
∵tanC=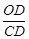
，
∴OD=CD·tanC=×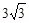
=3．
∴OC=2OD =6．
∵OB=OD=3，∴BC=OC-OB=6-3=3．
【解析】（1）根據切線的判定定理，連接OD，只需證明OD⊥CD，根據三角形的外角的性質得∠A=30°，再根據等邊對等角得∠ADO=∠A，從而證明結論；
（2）在30°的直角三角形OCD中，求得OD，OC的長，則BC=OC-OB．
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
如圖，在△ABC中，AB＞AC，E為BC邊的中點，AD為∠BAC的平分線，過E作AD的平行線，交AB于F，交CA的延長線于G．
如圖，在△ABC中，AB=AC，D為BC邊上一點，且∠BAD=30°，若AD=DE，∠EDC=33°，則∠DAE的度數為
如圖，在△ABC中，AB=AC，D是△ABC內一點，且BD=DC．求證：∠ABD=∠ACD．
如圖，在△ABC中，AB=BC，∠ABC=90°，D是BC的中點，且它關于AC的對稱點是D′，BD′=
如圖，在△ABC中，AB=AC，D點是BC的中點，DE⊥AB于E點，DF⊥AC于F點，則圖中全等三角形共有