如圖：在△ABC中，∠C＝90°，AD平分∠CAB，BC＝8cm，AC＝6cm，那么點D到AB的距離是____ ____cm．
3
【解析】
試題分析：過點D作DE⊥AB于點E，由∠C＝90°，AD平分∠CAB再結合公共邊AD可證得△ACD≌△AED，根據勾股定理可求得AB的長，從而可以得到BE的長，設CD=DE=x，在Rt△BED中，根據勾股定理列方程求解即可.
過點D作DE⊥AB于點E，
∵AD平分∠CAB
∴∠CAD=∠EAD
∵∠C＝∠AED=90°，AD=AD
∴△ACD≌△AED
∴AC=AE=6，CD=DE
∵∠C＝90°，BC＝8，AC＝6
∴
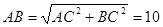
∴BE=ABAE=4
設CD=DE=x，則BD=8x
在Rt△BED中，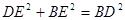
即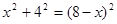
，解得
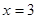
∴點D到AB的距離是3cm.
考點：1.角平分線的性質；2.勾股定理；3.全等三角形的判定和性質
閱讀快車系列答案科目：初中數學 來源： 題型：
如圖，在△ABC中，∠ACB=90°，AC=BC=1，取斜邊的中點，向斜邊作垂線，畫出一個新的等腰三角形，如此繼續(xù)下去，直到所畫出的直角三角形的斜邊與△ABC的BC重疊，這時這個三角形的斜邊為A、
| ||||
B、（
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
20、如圖，在△ABC中，∠BAC=45°，現將△ABC繞點A逆時針旋轉30°至△ADE的位置，使AC⊥DE，則∠B=
2、如圖，在△ABC中，DE∥BC，那么圖中與∠1相等的角是（ ）
如圖，在△ABC中，AB=AC，且∠A=100°，∠B=