
 校園內(nèi)有一個高大的樹,在實踐活動課上,準(zhǔn)備了如下測量工具“皮尺”、“高為1米的測角器”、“長為2米的標(biāo)桿”來測量樹的高度,請你設(shè)計測量方案并回答下列問題.
校園內(nèi)有一個高大的樹,在實踐活動課上,準(zhǔn)備了如下測量工具“皮尺”、“高為1米的測角器”、“長為2米的標(biāo)桿”來測量樹的高度,請你設(shè)計測量方案并回答下列問題.
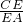 =
= ;即AB=
;即AB= .
.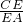 =
= ,即AB=
,即AB= .
.

 發(fā)散思維新課堂系列答案
發(fā)散思維新課堂系列答案科目:初中數(shù)學(xué) 來源: 題型:
 校園內(nèi)有一個高大的樹,在實踐活動課上,準(zhǔn)備了如下測量工具“皮尺”、“高為1米的測角器”、“長為2米的標(biāo)桿”來測量樹的高度,請你設(shè)計測量方案并回答下列問題.
校園內(nèi)有一個高大的樹,在實踐活動課上,準(zhǔn)備了如下測量工具“皮尺”、“高為1米的測角器”、“長為2米的標(biāo)桿”來測量樹的高度,請你設(shè)計測量方案并回答下列問題.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com