Question

（2012•中江縣二模）在平面直角坐標(biāo)系中，拋物線y=ax²+bx+c與x軸交于A、B兩點(diǎn)（點(diǎn)A在點(diǎn)B的左側(cè)），與y軸交于點(diǎn)C，點(diǎn)B的坐標(biāo)為（6，0），若將經(jīng)過B、C兩點(diǎn)的直線y=mx+n沿y軸向下平移6則恰好經(jīng)過原點(diǎn)，且拋物線的對(duì)稱軸是直線x=4．
（1）求拋物線及直線BC的解析式；
（2）如果P是線段BC上一點(diǎn)，設(shè)△ABP、△ACP的面積分別是S_△ABP、S_△ACP，且S_△ABP=

2

3

S_△ACP，求點(diǎn)P的坐標(biāo)；
（3）設(shè)⊙Q的半徑為2，圓心Q在拋物線上運(yùn)動(dòng)．則在運(yùn)動(dòng)過程中，是否存在圓Q與坐標(biāo)軸相切的情況，若存在，請(qǐng)求出圓心Q的坐標(biāo)，若不存在，請(qǐng)說明理由．
（4）在（3）的情況下，設(shè)⊙Q的半徑為r，是否存在與兩坐標(biāo)軸同時(shí)相切的圓，若存在，求出半徑r的值，若不存在，請(qǐng)說明理由．

Answer 1

分析：（1）根據(jù)直線平移的規(guī)律，求出C點(diǎn)坐標(biāo)，再根據(jù)函數(shù)對(duì)稱軸為x=4，與y軸交點(diǎn)坐標(biāo)為（0，6），利用待定系數(shù)法求出函數(shù)解析式；
（2）設(shè)P（x′，-x′+6），由S_△ABP=

2

3

S_△ACP得：S_△ABP=

2

3

（S_△ABC-S_△ABP），據(jù)此建立關(guān)于x′的方程，解方程即可求出函數(shù)解析式；
（3）分兩種情況討論：①當(dāng)⊙Q與y軸相切時(shí)，有|x₀|=2，即x₀=±2．據(jù)此求出y的值；②當(dāng)⊙Q與x軸相切時(shí)，有|y₀|=2，即y₀=±2．據(jù)此求出x的值．

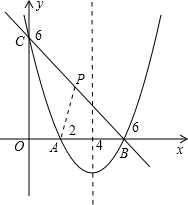解答：解：（1）直線y=mx+n沿y軸向下平移6后恰好經(jīng)過原點(diǎn)，
∴n=6，C（0，6）．
將B（6，0）代入y=mx+6，得mx+6=0，m=-1．
∴直線AC的解析式為y=-x+6．
∵拋物線y=ax²+bx+c過點(diǎn)A、C，且對(duì)稱軸x=4，c=6．
∴

36a+6b+c=0 - b 2a =4 c=6

，
解之得：

a= 1 2 b=-4 c=6

，
∴拋物線的函數(shù)解析式為y=

1

2

x2-4x+6．
注：變可設(shè)拋物線方程y=a（x-2）（x-6），代入C（0，6）即可求之．
（2）設(shè)P（x′，-x′+6），
由S_△ABP=

2

3

S_△ACP得：S_△ABP=

2

3

（S_△ABC-S_△ABP），
∴5S_△ABP=2S_△ABC．
5×

1

2

（6-2）（-x′+6）=2×

1

2

×（6-2）×6，
解之得：x′=

18

5

，
∴P（

18

5

，

12

5

）．
（3）假設(shè)⊙Q在運(yùn)動(dòng)過程中，存在⊙Q與坐標(biāo)軸相切的情況．
設(shè)點(diǎn)Q的坐標(biāo)為（x₀，y₀）．
①當(dāng)⊙Q與y軸相切時(shí)，有|x₀|=2，即x₀=±2．
當(dāng)x₀=-2時(shí)，
∴y0=

1

2

(-2)2-4×(-2)+6=16，
∴Q₁（-2，16）．
當(dāng)x₀=2時(shí)，y0=

1

2

×22-4×2+6=0，
∴Q₂（2，0）．
②當(dāng)⊙Q與x軸相切時(shí)，有|y₀|=2，即y₀=±2．
當(dāng)y₀=-2時(shí)，有

1

2

x02-4x0+6=-2，解之得x₀=4．
∴Q₃（4，-2）．
當(dāng)y₀=2時(shí)，有

1

2

x02-4x0+6=2，
解之得，x0=4±2

2

．
∴Q₄（4+2

2

，2），Q₅（4-2

2

，2）．
綜上所述，存在符合條件的⊙Q，其圓心Q的坐標(biāo)分別為Q₁（-2，16）、Q₂（2，0）、Q₃（4，-2）、Q₄（4+2

2

，2）、Q₅（4-2

2

，2）．
（4）存在與兩坐標(biāo)軸同時(shí)相切的圓．設(shè)點(diǎn)Q（x₁，y₁）．
當(dāng)⊙Q與兩坐標(biāo)軸同時(shí)相切時(shí)，有|y₁|=|x₁|=r，即y₁=±x₁．
由y₁=x₁，得

1

2

x12-4x1+6=x1，即x12-10x1+12=0，
解之得：x1=5±

13

．
∴r=5±

13

．
由y₁=-x₁，得

1

2

x12-4x1+6=-x1，
即x12-6x1+12=0．
此方程無實(shí)數(shù)解．
綜上所述，存在與兩坐標(biāo)軸同時(shí)相切的圓，此圓半徑r=5±

13

．

點(diǎn)評(píng)：此題考查了二次函數(shù)綜合題，涉及待定系數(shù)法求函數(shù)解析式、切線的判定和性質(zhì)，都用到了分類討論的數(shù)學(xué)思想，難點(diǎn)在于考慮問題要全面，做到不重不漏．