
 AC,同理可得IG∥BD,IG=
AC,同理可得IG∥BD,IG= BD,易求AC=BD,又由于GF∥AC,∠IGF=90°,利用平行線性質可得∠IHO=90°,而IG∥BD,易證∠BOC=90°,即AC⊥BD,從而可證四邊形ABCD的對角線互相垂直且相等.
BD,易求AC=BD,又由于GF∥AC,∠IGF=90°,利用平行線性質可得∠IHO=90°,而IG∥BD,易證∠BOC=90°,即AC⊥BD,從而可證四邊形ABCD的對角線互相垂直且相等.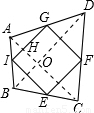 解:如右圖所示,四邊形ABCD的各邊中點分別是I、E、F、G,且四邊形EFGI是正方形,
解:如右圖所示,四邊形ABCD的各邊中點分別是I、E、F、G,且四邊形EFGI是正方形, AC,
AC, BD,
BD, AC=
AC= BD,
BD,

 發散思維新課堂系列答案
發散思維新課堂系列答案科目:初中數學 來源:2008年湖北省天門市中考數學試卷(解析版) 題型:選擇題
查看答案和解析>>
科目:初中數學 來源:2008年全國中考數學試題匯編《命題與證明》(01)(解析版) 題型:選擇題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com