
【題目】二次函數y=ax2+bx+c(a≠0)的部分圖象如圖所示,圖象過點(﹣1,0),對稱軸為直線x=2,下列結論:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若點A(﹣3,y1)、點B(﹣ ![]() ,y2)、點C(
,y2)、點C( ![]() ,y3)在該函數圖象上,則y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的兩根為x1和x2 , 且x1<x2 , 則x1<﹣1<5<x2 . 其中正確的結論有( )
,y3)在該函數圖象上,則y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的兩根為x1和x2 , 且x1<x2 , 則x1<﹣1<5<x2 . 其中正確的結論有( ) 
A.2個
B.3個
C.4個
D.5個
【答案】B
【解析】解:(1)正確.∵﹣ ![]() =2, ∴4a+b=0.故正確.(2)錯誤.∵x=﹣3時,y<0,
=2, ∴4a+b=0.故正確.(2)錯誤.∵x=﹣3時,y<0,
∴9a﹣3b+c<0,
∴9a+c<3b,故(2)錯誤.(3)正確.由圖象可知拋物線經過(﹣1,0)和(5,0),
∴ ![]() 解得
解得 ![]() ,
,
∴8a+7b+2c=8a﹣28a﹣10a=﹣30a,
∵a<0,
∴8a+7b=2c>0,故(3)正確.(4)錯誤,∵點A(﹣3,y1)、點B(﹣ ![]() ,y2)、點C(
,y2)、點C( ![]() ,y3),
,y3),
∵ ![]() ﹣2=
﹣2= ![]() ,2﹣(﹣
,2﹣(﹣ ![]() )=
)= ![]() ,
,
∴ ![]() <
< ![]()
∴點C離對稱軸的距離近,
∴y3>y2 ,
∵a<0,﹣3<﹣ ![]() <2,
<2,
∴y1<y2
∴y1<y2<y3 , 故(4)錯誤.(5)正確.∵a<0,
∴(x+1)(x﹣5)=﹣3/a>0,
即(x+1)(x﹣5)>0,
故x<﹣1或x>5,故(5)正確.
∴正確的有三個,
故選B.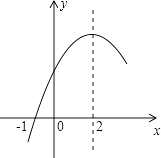
【考點精析】掌握二次函數圖象以及系數a、b、c的關系是解答本題的根本,需要知道二次函數y=ax2+bx+c中,a、b、c的含義:a表示開口方向:a>0時,拋物線開口向上; a<0時,拋物線開口向下b與對稱軸有關:對稱軸為x=-b/2a;c表示拋物線與y軸的交點坐標:(0,c).


科目:初中數學 來源: 題型:
【題目】南縣農民一直保持著冬種油菜的習慣,利用農閑冬種一季油菜.南縣農業部門對2009年的油菜籽生產成本、市場價格、種植面積和產量等進行了調查統計,并繪制了如下統計表與統計圖:請根據以上信息解答下列問題
(1)種植油菜每畝的種子成本是多少元?
(2)農民冬種油菜每畝獲利多少元?
(3)2009年南縣全縣農民冬種油菜的總獲利多少元?(結果用科學記數法表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在求![]() 的值時,小林發現:從第二個加數起每一個加數都是前一個加數的6倍,于是她設:
的值時,小林發現:從第二個加數起每一個加數都是前一個加數的6倍,于是她設:![]() ……①
……①
然后在①式的兩邊都乘以6,得:![]() ……②
……②
②-①得![]() ,即
,即![]() ,所以
,所以![]() .
.
得出答案后,愛動腦筋的小林想:如果把“6”換成字母“a”(a≠0且a≠1),能否求出![]() 的值?你的答案是
的值?你的答案是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=1,與x軸的一個交點坐標為(﹣1,0),其部分圖象如圖所示,下列結論:
①4ac<b2;
②方程ax2+bx+c=0的兩個根是x1=﹣1,x2=3;
③3a+c>0
④當y>0時,x的取值范圍是﹣1≤x<3
⑤當x<0時,y隨x增大而增大
其中結論正確的個數是( )
A.4個
B.3個
C.2個
D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數y=(2m-3)x+m+2.
(1)若函數圖像過原點,求m的值;
(2)若函數圖像過點(-1,0),求m的值;
(3)若函數圖像平行于直線y=-x+2求m的值;
(4)若函數圖像經過第一、二、四象限,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,有若干個橫縱坐標分別為整數的點,其順序為(1,0)、(2, 0)、(2,1)、(1,1)、(1,2)、(2,2)…根據這個規律,第2019個點的坐標為( )

A. (45,6)B. (45,13)C. (45,22)D. (45,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種小商品的成本價為10元/kg,市場調查發現,該產品每天的銷售量w(kg)與銷售價x(元/kg)有如下關系w=﹣2x+100,設這種產品每天的銷售利潤為y(元).
(1)求y與x之間的函數關系式;
(2)當售價定為多少元時,每天的銷售利潤最大?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com