
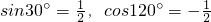 ,所以
,所以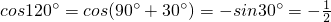 ,
,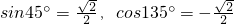 ,所以
,所以 ,
,科目:初中數學 來源: 題型:閱讀理解
閱讀材料:已知p2-p-1=0 , 1-q-q2=0, 且pq≠1 ,求![]() 的值.
的值.
解:由p2-p-1=0及1-q-q2=0,可知p≠0,q≠0,
又因為pq≠1 所以p≠![]() ,所以1-q-q2 =0可變形為:(
,所以1-q-q2 =0可變形為:(![]() )2-(
)2-(![]() )-1=0 ,
)-1=0 ,
根據p2-p-1=0和(![]() )2-(
)2-(![]() )-1=0的特征,
)-1=0的特征,
p與![]() 可以看作方程x2-x-1=0的兩個不相等的實數根,所以p+
可以看作方程x2-x-1=0的兩個不相等的實數根,所以p+![]() =1, 所以
=1, 所以![]() =1.
=1.
根據以上閱讀材料所提供的方法,完成下面的解答:
1.已知m2-5mn+6n2=0,m>n,求![]() 的值
的值
2.已知2m2-5m-1=0,(![]() )2+
)2+ -2=0,且m≠n ,求
-2=0,且m≠n ,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
 的值.
的值. ,所以1-q-q2 =0可變形為:(
,所以1-q-q2 =0可變形為:( )2-(
)2-( )-1=0 ,
)-1=0 , )2-(
)2-( )-1=0的特征,
)-1=0的特征, 可以看作方程x2-x-1=0的兩個不相等的實數根,所以p+
可以看作方程x2-x-1=0的兩個不相等的實數根,所以p+ =1, 所以
=1, 所以 =1.
=1. 的值
的值 )2+
)2+ -2=0,且m≠n ,求
-2=0,且m≠n ,求 的值.
的值.查看答案和解析>>
科目:初中數學 來源:2013屆江蘇泰州中學附屬初中九年級第一次考試數學試卷(帶解析) 題型:解答題
配方法可以用來解一元二次方程,還可以用它來解決很多問題。例如:因為 ,所以
,所以 ,即:
,即: 有最小值1,此時
有最小值1,此時 ;同樣,因為
;同樣,因為 ,所以
,所以 ,即
,即 有最大值6,此時
有最大值6,此時 。
。
①當 = 時,代數式
= 時,代數式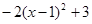 有最 (填寫大或小)值為 。②當
有最 (填寫大或小)值為 。②當 = 時,代數式
= 時,代數式 有最 (填寫大或小)值為 。
有最 (填寫大或小)值為 。
③矩形花園的一面靠墻,另外三面的柵欄所圍成的總長度是16m,當花園與墻相鄰的邊長為多少時,花園的面積最大?最大面積是多少?
查看答案和解析>>
科目:初中數學 來源:2012-2013學年江蘇泰州中學附屬初中九年級第一次考試數學試卷(解析版) 題型:解答題
配方法可以用來解一元二次方程,還可以用它來解決很多問題。例如:因為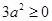 ,所以
,所以 ,即:
,即: 有最小值1,此時
有最小值1,此時 ;同樣,因為
;同樣,因為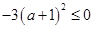 ,所以
,所以 ,即
,即 有最大值6,此時
有最大值6,此時  。
。
①當 =
時,代數式
=
時,代數式 有最 (填寫大或小)值為
。②當
有最 (填寫大或小)值為
。②當 =
時,代數式
=
時,代數式 有最 (填寫大或小)值為
。
有最 (填寫大或小)值為
。
③矩形花園的一面靠墻,另外三面的柵欄所圍成的總長度是16m,當花園與墻相鄰的邊長為多少時,花園的面積最大?最大面積是多少?

查看答案和解析>>
科目:初中數學 來源:2011-2012學年廣東珠海紫荊中學一模數學試卷(解析版) 題型:解答題
閱讀材料:已知p2-p-1=0 , 1-q-q2=0
, 且pq≠1 ,求 的值.
的值.
解:由p2-p-1=0及1-q-q2=0,可知p≠0,q≠0,
又因為pq≠1 所以p≠ ,所以1-q-q2 =0可變形為:(
,所以1-q-q2 =0可變形為:( )2-(
)2-( )-1=0 ,
)-1=0 ,
根據p2-p-1=0和( )2-(
)2-( )-1=0的特征,
)-1=0的特征,
p與 可以看作方程x2-x-1=0的兩個不相等的實數根,所以p+
可以看作方程x2-x-1=0的兩個不相等的實數根,所以p+ =1, 所以
=1, 所以 =1.
=1.
根據以上閱讀材料所提供的方法,完成下面的解答:
1.已知m2-5mn+6n2=0,m>n,求 的值
的值
2.已知2m2-5m-1=0,( )2+
)2+ -2=0,且m≠n ,求
-2=0,且m≠n ,求 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com