某批發商以每件50元的價格購進500件T恤.若以單價70元銷售,預計可售出200件.批發商的銷售策略是:第一個月為增加銷售量,降價銷售,經過市場調查,單價每降低1元,可多售出10件,但最低單價高于購進的價格;第一個月結束后,將剩余的T恤一次性清倉銷售,清倉時單價為40元.
(1)按照批發商的銷售策略,銷售完這批T恤可能虧本嗎?請建立函數關系進行說明;
(2)從增加銷售量的角度看,第一個月批發商降價多少元時,銷售完這批T恤獲得的利潤為1000元?
【答案】
分析:(1)根據題意直接用含x的代數式表示出銷量以及每件利潤即可得出答案;
(2)利用“獲利1000元”,即銷售額-進價=利潤,作為相等關系列方程,解方程求解后要代入實際問題中檢驗是否符合題意,進行值的取舍.
解答:解:(1)解法一:設第一個月單價降低x元,批發商銷售完這批T恤獲得的總利潤為y元.
根據題意,得y=(70-50-x)(200+10x)+(40-50)×[500-(200+10x)]
=-10x
2+100x+1000.
批發商銷售這批T恤可能虧本,理由如下:(答案不唯一,以下方法供參考)
方法一:當x=17(或18或19)時,y<0.
方法二:當y=0時,x=5
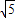
+5(負根舍去).
又因為當5
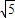
+5<x<20時,y隨x的增大而減小,
所以當x=17或18或19時,y<0.
解法二:設第一個月單價降低x元,當月出售T恤獲得的利潤為y
1元,清倉剩余T恤獲得的利潤為y
2元.
根據題意,得y
1=(70-50-x)(200+10x)=-10x
2+4000,
y
2=(40-50)×[500-(200+10x)]=100x-3000.
批發商銷售這批T恤可能虧本,理由如下:(答案不唯一,以下方法供參考)
方法一:當x=17(或18或19)時,y
1+y
2<0.
方法二:當y
1+y
2=0時,x=5
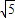
+5(負根舍去).
又因為當5
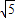
+5<x<20時,y
1+y
2隨x的增大而減小,
所以當x=17或18或19時,y
1+y
2<0.
(2)設第一個月單價降低x元時,銷售完這批T恤獲得的利潤為1000元.
根據題意得-10x
2+100x+1000=1000.
解這個方程,得x
1=0,x
2=10.
從增加銷售量的角度看,取x=10.
答:第一個月單價降低10元時,銷售完這批T恤獲得的利潤為1000元.
點評:此題主要考查了二次函數的應用,解題關鍵是要讀懂題目的意思,根據題目給出的條件,找出合適的等量關系,列出方程,再求解.有關銷售問題中的等量關系一般為:利潤=售價-進價.

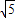 +5(負根舍去).
+5(負根舍去).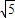 +5<x<20時,y隨x的增大而減小,
+5<x<20時,y隨x的增大而減小,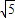 +5(負根舍去).
+5(負根舍去).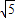 +5<x<20時,y1+y2隨x的增大而減小,
+5<x<20時,y1+y2隨x的增大而減小,

 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案
