Question

4．將兩塊全等的直角三角形紙片△ABC和△DEF疊放在一起，其中∠ACB=∠E=90°，BC=DE=6，AC=FE=8，點D與邊AB的中點重合，將△DEF繞著點D旋轉．
（1）如圖1，如果∠EDF的邊DE經過點C，另一邊DF與邊AC交于點G，求GC的長；
（2）如圖2，如果∠EDF的邊DF、DE分別交邊BC于點M、N，設CN=x、BM=y，求y關于x的函數解析式，并求它的定義域；
（3）如圖3，如果∠EDF的邊DF、DE分別交邊AC于點M、N，如果△DMN是等腰三角形，求AN的值．

Answer 1

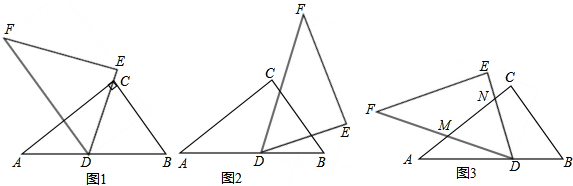
分析 （1）先判定三角形ACD是等腰三角形，再判定DG⊥AC，最后根據三線合一求得GC的長；
（2）先連接CD，再判定△DNC∽△MDB，最后根據相似三角形對應邊成比例，列出比例式并變形，即可得到函數關系式以及定義域；
（3）根據△DMN是等腰三角形，需要分三種情況進行討論，分別求得AN的長即可．

解答 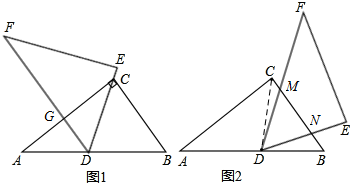解：（1）如圖1，∵△ABC≌△FDE，
∴∠GDC=∠B，
∵點D是邊AB的中點，
∴CD=AD=BD=$\frac{1}{2}$AB，
∴∠DCB=∠B，
∴∠GDC=∠DCB，
∴BC∥DG，
∴∠AGD=∠ACB=90°，
∵AD=CD，
∴GC=$\frac{1}{2}$AC=4；

（2）如圖2，連接CD，
在直角三角形ABC中，由勾股定理可得AB=10，
∵點D為AB的中點，∠ACB=90°，
∴BD=CD=$\frac{1}{2}$AB=5，
∴∠B=∠DCN，①
∵∠CND=∠B+∠BDN，∠BDM=∠MDN+∠BDN，且∠B=∠MDN，
∴∠CND=∠BDM，②
由①②可得△DNC∽△MDB，
∴$\frac{CD}{BM}$=$\frac{CN}{BD}$，即$\frac{5}{y}$=$\frac{x}{5}$，
∴$y=\frac{25}{x}$，
∵DF、DE分別交線段BC于點M、N，
∴CN≤CB，BM≤BC，
∴x≤6，y≤6即$\frac{25}{x}$≤6，
解得$\frac{25}{6}$≤x≤6；

（3）△DMN是等腰三角形，分三種情況：
①如圖3，當DM=MN時，∠MND=∠MDN=∠B，
由∠B+∠A=90°，可得∠DNM+∠A=90°，即ND⊥AD，
∴∠ADN=∠C=90°，
又∵∠A=∠A，
∴△ADN∽△ACB，
∴$\frac{DN}{CB}$=$\frac{AD}{AC}$，即$\frac{DN}{6}$=$\frac{5}{8}$，
∴DN=$\frac{15}{4}$，
∴直角三角形ADN中，AN=$\sqrt{{5}^{2}+（\frac{15}{4}）^{2}}$=$\frac{25}{4}$，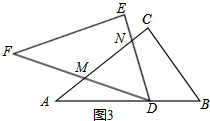

②如圖4，當NM=ND時，∠DMH=∠MDN=∠B，
過D作DH⊥MN于H，則∠DHM=∠C=90°，DH=$\frac{1}{2}$BC=3，
∴△DHM∽△ACB，
∴$\frac{MH}{BC}$=$\frac{DH}{AC}$，即$\frac{MH}{6}$=$\frac{3}{8}$，
∴MH=$\frac{9}{4}$，
∴DN=MN=$\frac{9}{4}$+HN，
∴直角三角形DHN中，HN²+HD²=DN²，即HN²+3²=（$\frac{9}{4}$+HN）²，
解得HN=$\frac{7}{8}$，
又∵直角三角形ADH中，AH=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴AN=AH+HN=4+$\frac{7}{8}$=$\frac{39}{8}$，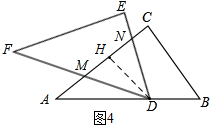

③如圖5，當DN=DM時，設DN=DM=y，MN=2x，
過D作DH⊥MN于H，則MH=NH=$\frac{1}{2}$MN=x，
過N作NQ⊥MD于Q，則∠NQD=∠C=90°，
∵∠NDQ=∠B，
∴△NDQ∽△ABC，
∴$\frac{ND}{AB}$=$\frac{NQ}{AC}$，即$\frac{y}{10}$=$\frac{NQ}{8}$，
∴NQ=$\frac{4}{5}$y，
∵$\frac{1}{2}$×MN×DH=$\frac{1}{2}$×DM×NQ，
∴2x×3=y×$\frac{4}{5}$y，即y²=$\frac{30}{4}$x，
又∵直角三角形DHN中，DN²=DH²+HN²，即y²=3²+x²
∴$\frac{30}{4}$x=3²+x²
解得x₁=1.5，x₂=6（舍去），
∴HN=1.5
又∵直角三角形ADH中，AH=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴AN=AH+HN=4+1.5=$\frac{11}{2}$，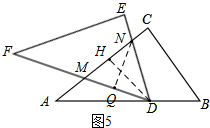

故AN的值為：$\frac{25}{4}$或$\frac{39}{8}$或$\frac{11}{2}$．

點評 本題以旋轉變換為背景，考查了等腰三角形的性質以及相似三角形的判定與性質．在解決等腰三角形的問題時，一般需要作輔助線，運用三線合一的性質進行求解，有時需要進行分類討論，分類時要注意不能遺漏，不能重復．