Question

【題目】如圖1，△ABC和△DEF中，AB=AC，DE=DF，∠A=∠D.

（1）求證： .

（2）由（1）中的結論可知，等腰三角形ABC中，當頂角∠A的大小確定時，它的對邊（即底邊BC）與鄰邊（即腰AB或AC）的比值也就確定，我們把這個比值記作T(A)，即

，如T(60°)=1.

①理解鞏固：T(90°)= ________，T(120°)=_________，若α是等腰三角形的頂角，則T(α)的取值范圍是_____________________；

②學以致用：如圖2，圓錐的母線長為9，底面直徑PQ=8，一只螞蟻從點這沿著圓錐的側面爬行到點Q，求螞蟻爬行的最短路徑長（精確到0.1）.

（參考數據：T(160°)≈1.97，T(80°)≈1.29，T(40°)≈0.68）

Answer 1

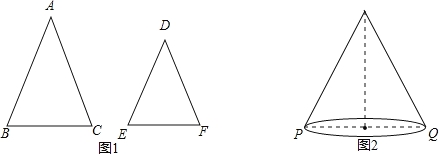
【答案】 0＜T（α）＜2

【解析】試題分析：（1）證明△ABC∽△DEF，根據相似三角形的性質解答即可；

（2）①根據等腰直角三角形的性質和等腰三角形的性質進行計算即可；

②根據圓錐的側面展開圖的知識和扇形的弧長公式計算，得到扇形的圓心角，根據T（A）的定義解答即可．

（1）∵AB=AC，DE=DF，∴ ，又∵∠A=∠D，∴△ABC∽△DEF，∴；

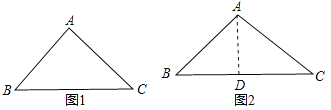
（2）①如圖1，∠A=90°，AB=AC，則=，∴T（90°）=，如圖2，∠A=90°，AB=AC，作AD⊥BC于D，則∠B=60°，∴BD=AB，∴BC=AB，∴T（120°）=；

∵AB﹣AC＜BC＜AB+AC，∴0＜T（α）＜2，故答案為： ； ；0＜T（α）＜2；

②∵圓錐的底面直徑PQ=8，∴圓錐的底面周長為8π，即側面展開圖扇形的弧長為8π，設扇形的圓心角為n°，則=8π，解得，n=160，∵T（80°）≈1.29，∴螞蟻爬行的最短路徑長為1.29×9≈11.6．