
【題目】已知,m,n是一元二次方程![]() 的兩個實數根,且|m|<|n|,拋物線
的兩個實數根,且|m|<|n|,拋物線![]() 的圖象經過點A(m,0),B(0,n),如圖所示.
的圖象經過點A(m,0),B(0,n),如圖所示.
(1)求這個拋物線的解析式;
(2)設(1)中的拋物線與x軸的另一個交點為拋物線的頂點為D,試求出點C,D的坐標,并判斷△BCD的形狀;
(3)點P是直線BC上的一個動點(點P不與點B和點C重合),過點P作x軸的垂線,交拋物線于點M,點Q在直線BC上,距離點P為![]() 個單位長度,設點P的橫坐標為t,△PMQ的面積為S,求出S與t之間的函數關系式.
個單位長度,設點P的橫坐標為t,△PMQ的面積為S,求出S與t之間的函數關系式.

【答案】(1)![]() ;(2)△BCD是直角三角形;(3)S=
;(2)△BCD是直角三角形;(3)S=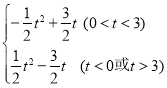 .
.
【解析】
試題分析:(1)先解一元二次方程,然后用待定系數法求出拋物線解析式;
(2)先解方程求出拋物線與x軸的交點,再判斷出△BOC和△BED都是等腰直角三角形,從而得到結論;
(3)先求出QF=1,再分兩種情況,當點P在點M上方和下方,分別計算即可.
試題解析:解(1)∵![]() ,∴
,∴![]() ,
,![]() ,∵m,n是一元二次方程
,∵m,n是一元二次方程![]() 的兩個實數根,且|m|<|n|,∴m=﹣1,n=﹣3,∵拋物線
的兩個實數根,且|m|<|n|,∴m=﹣1,n=﹣3,∵拋物線![]() 的圖象經過點A(m,0),B(0,n),∴
的圖象經過點A(m,0),B(0,n),∴![]() ,∴
,∴![]() ,∴拋物線解析式為
,∴拋物線解析式為![]() ;
;
(2)令y=0,則![]() ,∴
,∴![]() ,
,![]() ,∴C(3,0),∵
,∴C(3,0),∵![]() =
=![]() ,∴頂點坐標D(1,﹣4),過點D作DE⊥y軸,∵OB=OC=3,∴BE=DE=1,∴△BOC和△BED都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD是直角三角形;
,∴頂點坐標D(1,﹣4),過點D作DE⊥y軸,∵OB=OC=3,∴BE=DE=1,∴△BOC和△BED都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD是直角三角形;
(3)如圖,∵B(0,﹣3),C(3,0),∴直線BC解析式為y=x﹣3,∵點P的橫坐標為t,PM⊥x軸,∴點M的橫坐標為t,∵點P在直線BC上,點M在拋物線上,∴P(t,t﹣3),M(t,![]() ),過點Q作QF⊥PM,∴△PQF是等腰直角三角形,∵PQ=
),過點Q作QF⊥PM,∴△PQF是等腰直角三角形,∵PQ=![]() ,∴QF=1.
,∴QF=1.
①當點P在點M上方時,即0<t<3時,PM=t﹣3﹣(![]() )=
)=![]() ,∴S=
,∴S=![]() PM×QF=
PM×QF=![]() =
=![]() ,②如圖3,當點P在點M下方時,即t<0或t>3時,PM=
,②如圖3,當點P在點M下方時,即t<0或t>3時,PM=![]() ﹣(t﹣3)=
﹣(t﹣3)=![]() ,∴S=
,∴S=![]() PM×QF=
PM×QF=![]() (
(![]() )=
)=![]() .
.
綜上所述,S=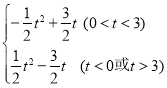 .
.


科目:初中數學 來源: 題型:
【題目】已知,拋物線![]() ( a≠0)經過原點,頂點為A ( h,k ) (h≠0).
( a≠0)經過原點,頂點為A ( h,k ) (h≠0).
(1)當h=1,k=2時,求拋物線的解析式;
(2)若拋物線![]() (t≠0)也經過A點,求a與t之間的關系式;
(t≠0)也經過A點,求a與t之間的關系式;
(3)當點A在拋物線![]() 上,且-2≤h<1時,求a的取值范圍.
上,且-2≤h<1時,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
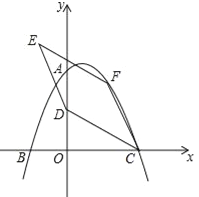
【題目】如圖,在平面直角坐標系中,二次函數![]() 的圖象與坐標軸交于A、B、C三點,其中點A的坐標為(0,8),點B的坐標為(﹣4,0).
的圖象與坐標軸交于A、B、C三點,其中點A的坐標為(0,8),點B的坐標為(﹣4,0).
(1)求該二次函數的表達式及點C的坐標;
(2)點D的坐標為(0,4),點F為該二次函數在第一象限內圖象上的動點,連接CD、CF,以CD、CF為鄰邊作平行四邊形CDEF,設平行四邊形CDEF的面積為S.
①求S的最大值;
②在點F的運動過程中,當點E落在該二次函數圖象上時,請直接寫出此時S的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題7分)數學課上,探討角平分線的作法時,李老師用直尺和圓規作角平分線,方法如下:
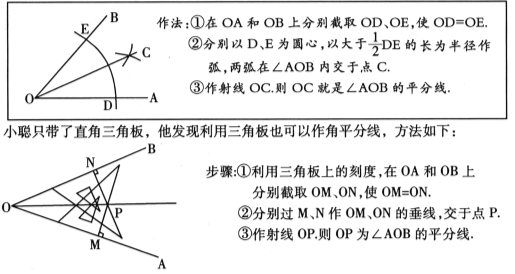
根據以上情境,解決下列問題:
(1)李老師用尺規作角平分線時,用到的三角形全等的判定方法是 .
(2)小聰的作法正確嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
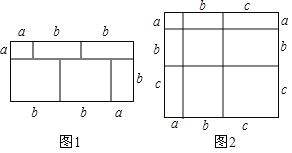
【題目】當我們利用2種不同的方法計算同一圖形的面積時,可以得到一個等式.例如,由圖1可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由圖2,可得等式:_____________________________
(2)利用(1)中所得到的結論,解決下面的問題:
已知 a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com