
【題目】為了激發學生愛數學、學數學、用數學的熱情,某學校在七年級開展“魅力數學”趣味競賽,該校七年級共有學生400人參加競賽.現隨機抽取40名參賽學生的成績數據(百分制)進行整理、描述和分析.
74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
范圍 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
頻數 | 1 | m | 13 | 9 | 14 |
平均數、中位數、眾數如下表所示:
平均數 | 中位數 | 眾數 |
84.1 | n | 89 |
根據以上信息,回答下列問題:
(1)m= ,n= ;
(2)小明說:“這次競賽我得了84分,在所有參賽學生中排名屬中等偏上!”小明的說法 (填“正確”或“不正確”),理由是 ;
(3)若成績不低于85分可以進入決賽,估計參賽的400名學生中能進入決賽的人數.
【答案】(1)m=3,n=88;(2)不正確,中位數為88,84<88;(3)230.
【解析】
(1)用40減去各個范圍的人數可求m,這組數據的個數是偶數,則中間兩個數據的平均數就是這組數據的中位數.
(2)小明得了84分,略低于競賽成績樣本數據的中位數88,說明小亮的成績排名屬中等偏下.
(3)根據競賽成績不低于85分的人數為17,即可估計參賽的400名學生中能進入決賽的人數.
(1)m=40﹣1﹣13﹣9﹣14=3,
從小到大排列,第20和21個數都是88,中位數n=88;
(2)小明說:“這次競賽我得了84分,在所有參賽學生中排名屬中等偏上!”
小明的說法 不正確,理由是 中位數為88,84<88;
(3)400×![]() =230(人).
=230(人).
故估計參賽的400名學生中能進入決賽的人數為230人.
故答案為:3;88;不正確;中位數為88,84<88.


科目:初中數學 來源: 題型:
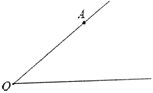
【題目】如圖,點![]() 在
在![]() 的一邊
的一邊![]() 上,按要求畫圖并填空:
上,按要求畫圖并填空:
(1)過點![]() 畫直線
畫直線![]() ,與
,與![]() 的另一邊相交于點
的另一邊相交于點![]() ;
;
(2)過點![]() 畫
畫![]() 的垂線
的垂線![]() ,垂足為點
,垂足為點![]() ;
;
(3)過點![]() 畫直線
畫直線![]() ,交直線
,交直線![]() 于點
于點![]() ;
;
(4)直接寫出![]() _____
_____![]() ;
;
(5)如果![]() ,
,![]() ,
,![]() ,那么點
,那么點![]() 到直線
到直線![]() 的距離為_______.
的距離為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點A(1,2)、點 B在雙曲線y= ![]() (x>0)上,過B作BC⊥x軸于點C,如圖,P是y軸上一點,
(x>0)上,過B作BC⊥x軸于點C,如圖,P是y軸上一點,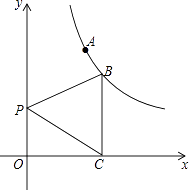
(1)求k的值及△PBC的面積;
(2)設點M(x1 , y1)、N(x2 , y2)(x2>x1>0)是雙曲線y= ![]() (x>0)上的任意兩點,s=
(x>0)上的任意兩點,s= ![]() ,t=
,t= ![]() ,試判斷s與t的大小關系,并說明理由.
,試判斷s與t的大小關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】送報員李師傅騎摩托車從報社出發,先向西行駛3千米到達A村,繼續向西行駛2千米到達B村,然后向東行駛10千米到達C村,最后回到報社.
(1)若把李師傅的出發地記為0(即以報社為原點),以向東方向為正方向,在數軸上表示出A、B、C三個村莊的位置;
(2)A、C兩個村莊相距多遠?
(3)送報員李師傅一共騎行了多少千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
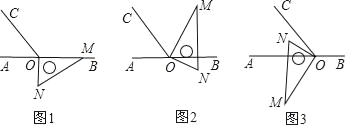
【題目】如圖1,點O為直線AB上一點,過點O作射線OC,使∠BOC=112°.將一直角三角板的直角頂點放在點O處,一邊OM在射線OB上,另一邊ON在直線AB的下方.
(1)將圖1中的三角板繞點O逆時針旋轉至圖2,使一邊OM在∠BOC的內部,且恰好平分∠BOC,問:射線ON是否平分∠AOC?請說明理由;
(2)將圖1中的三角板繞點O按每秒4°的速度沿逆時針方向旋轉至圖3,使射線ON恰好平分銳角∠AOC,求此時旋轉一共用了多少時間?
(3)將圖1中的三角板繞點O順時針旋轉至圖3,使ON在∠AOC的內部,請探究:∠AOM與∠NOC之間的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】假設我市出租車收費標準是:起步價6元,可乘3千米;3千米到5千米,每千米1.6元;超過5千米,每千米2.4元.
(1)若某人乘坐的路程為4千米,那么他支付的費用是多少?
(2)若某人乘坐了x(x>5)千米的路程,則他應支付的費用是多少?
(3)若某人乘坐的路程為10千米,那么他應支付的費用是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】利用圖1,圖2提供的某公司的一些信息,解答下列問題.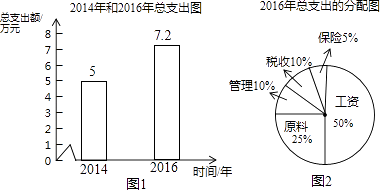
(1)2016年該公司工資支出的金額是萬元;
(2)2014年到2016年該公司總支出的年平均增長率;
(3)若保持這種增長速度,請你預估該公司2017年的總支出.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,在△ABC中,D是BC的中點,DE⊥BC,垂足為D,交AB于點E,且BE2-EA2=AC2,
(1)求證:∠A=90°.
(2)若DE=3,BD=4,求AE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題背景:(1)已知A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐標系中描出這幾個點,并分別找到線段AB和CD中點P1、P2,然后寫出它們的坐標,則P1 ,P2 .
探究發現:(2)結合上述計算結果,你能發現若線段的兩個端點的坐標分別為(x1,y1),(x2,y2),則線段的中點坐標為 .
拓展應用:(3)利用上述規律解決下列問題:已知三點E(﹣1,2),F(3,1),G(1,4),第四個點H(x,y)與點E、點F、點G中的一個點構成的線段的中點與另外兩個端點構成的線段的中點重合,求點H的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com