
【題目】問題一:如圖①,已知AC=160km,甲,乙兩人分別從相距30km的A,B兩地同時出發到C地.若甲的速度為80km/h,乙的速度為60km/h,設乙行駛時間為x(h),兩車之間距離為y(km).
(1)當甲追上乙時,x= .
(2)請用x的代數式表示y.
問題二:如圖②,若將上述線段AC彎曲后視作鐘表外圍的一部分,線段AB正好對應鐘表上的弧AB(1小時的間隔),易知∠AOB=30°.
(3)分針OD指向圓周上的點的速度為每分鐘轉動 km,時針OE指向圓周上的點的速度為每分鐘轉動 °;
(4)若從2:00起計時,求幾分鐘后分針與時針第一次重合?

【答案】(1)1.5h;(2)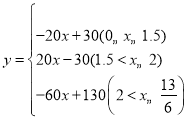 ;(3)6,0.5;(4)
;(3)6,0.5;(4)![]() 分鐘
分鐘
【解析】
(1)根據兩車間的距離=速度之差×時間,即可得出關于x的一元一次方程,解之即可得出結論;
(2)分0≤x≤1.5、1.5<x≤2、2<x≤![]() 三種情況找出y關于x的函數關系式;
三種情況找出y關于x的函數關系式;
(3)根據速度=路程÷時間,即可求出結論;
(4)設經歷t分鐘后分針和時針第一次重合,根據分針比時針多跑了60km,即可得出關于t的一元一次方程,解之即可得出結論.
解:(1)根據題意得:(80-60)x=30,
解得:x=1.5.
故答案為:1.5h.
(2)甲到達C需要的時間為:![]() h,
h,
乙到達C需要的時間為:![]() h,
h,
分三種情況:
當0≤x≤1.5時,y=30-(80-60)x=-20x+30,
當1.5<x≤2時,y=80x-(60x+30)=20x-30,
當2<x≤![]() 時,y=160-60x-30=-60x+130,
時,y=160-60x-30=-60x+130,
∴兩車之間的距離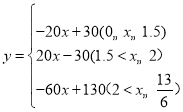 ;
;
(3)30÷5=6(km),
30÷60=0.5°,
故答案為:6;0.5;
(4)設經歷t分鐘后分針和時針第一次重合,
時針的速度為:30÷60=0.5千米/分
根據題意得:6t-0.5t=30×2,
解得:t=![]() ,
,
答:從2:00起計時,![]() 分鐘后分針與時針第一次重合.
分鐘后分針與時針第一次重合.


 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:初中數學 來源: 題型:
【題目】探究:如圖,直線 AB、BC、AC 兩兩相交,交點分別為點 A、B、C,點 D 在線段 AB 上,過點 D 作 DE∥BC 交 AC 于點 E,過點 E 作 EF∥AB 交 BC 于點 F.若∠ABC=40°,求∠DEF 的度數. 請將下面的解答過程補充完整,并填空(理由或數學式)

解:∵DE∥BC,( )
∴∠DEF= .( )
∵EF∥AB,
∴ =∠ABC.( )
∴∠DEF=∠ABC.( )
∵∠ABC=40°,
∴∠DEF= °.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知E、F是□ABCD對角線AC上的兩點,且BE⊥AC,DF⊥AC.

(1)請寫出圖中全等三角形(不再添加輔助線).
(2)求證:△ABE≌△CDF;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:已知方程a2![]() 2a
2a![]() 1=0,1
1=0,1![]() 2b
2b![]() b2=0且ab≠1,求
b2=0且ab≠1,求![]() 的值.
的值.
解:由a2![]() 2a
2a![]() 1=0及1
1=0及1![]() 2b
2b![]() b2=0,
b2=0,
可知a≠0,b≠0,
又∵ab≠1,![]() .
.
1![]() 2b
2b![]() b2=0可變形為
b2=0可變形為
![]() ,
,
根據a2![]() 2a
2a![]() 1=0和
1=0和![]() 的特征.
的特征.
![]() 、
、![]() 是方程x2
是方程x2![]() 2x
2x![]() 1=0的兩個不相等的實數根,
1=0的兩個不相等的實數根,
則![]() ,即
,即![]() .
.
根據閱讀材料所提供的方法,完成下面的解答.
已知:3m2![]() 7m
7m![]() 2=0,2n2+7n
2=0,2n2+7n![]() 3=0且mn≠1,求
3=0且mn≠1,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:△ABC在坐標平面內,三個頂點的坐標分別為A(0,3),B(3,4),C(2,2).(正方形網格中,每個小正方形的邊長是1個單位長度)
(1)作出△ABC繞點A順時針方向旋轉90°后得到的△A1B1C1,并寫出C1點的坐標 ;
(2)作出△ABC關于原點O成中心對稱的△A2B2C2,并求出△ABC的面積 .

查看答案和解析>>
科目:初中數學 來源: 題型:
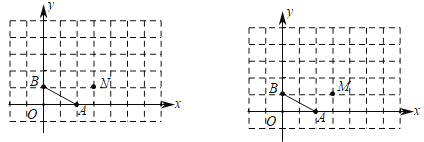
【題目】如圖,點![]() 的坐標分別為
的坐標分別為![]() ,將線段
,將線段![]() 直接平移到
直接平移到![]() ,使點
,使點![]() 移至點
移至點![]() 的位置,點
的位置,點![]() 移至點
移至點![]() 的位置,設平移過程中線段
的位置,設平移過程中線段![]() 掃過的面積為
掃過的面積為![]() ,
,
(1)如圖1,若點![]() 的坐標是
的坐標是![]() ,則點
,則點![]() 的坐標為_____________,請畫出平移后的線段
的坐標為_____________,請畫出平移后的線段![]() ;
;
(2)如圖2,若點![]() 的坐標是
的坐標是![]() ,請畫出平移后的線段
,請畫出平移后的線段![]() ,則
,則![]() 的值為_____________;
的值為_____________;
(3)若![]() ,且點
,且點![]() 在坐標軸上,請直接寫出所有滿足條件的
在坐標軸上,請直接寫出所有滿足條件的![]() 點的坐標.
點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com