
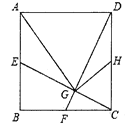
【題目】如圖,正方形![]() 中,點
中,點![]() 、
、![]() 、
、![]() 分別足
分別足![]() 、
、![]() ,
,![]() 的中點,
的中點,![]() 、
、![]() 交于
交于![]() ,連接
,連接![]() 、
、![]() .下列論:①
.下列論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正確的有( )
.其中正確的有( )
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
【答案】C
【解析】
連接AH,由四邊形ABCD是正方形與點E、F、H分別是AB、BC、CD的中點,易證得△BCE≌△CDF與△ADH≌△DCF,根據全等三角形的性質,易證得CE⊥DF與AH⊥DF,根據垂直平分線的性質,即可證得AG=AD,由直角三角形斜邊上的中線等于斜邊的一半,即可證得HG=![]() AD,根據等腰三角形的性質,即可得∠CHG=∠DAG.則問題得解.
AD,根據等腰三角形的性質,即可得∠CHG=∠DAG.則問題得解.
解:∵四邊形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=90°,
∵點E、F、H分別是AB、BC、CD的中點,
∴BE=CF,
在△BCE與△CDF中,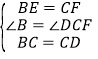
∴△BCE≌△CDF(SAS),
∴∠ECB=∠CDF,
∵∠BCE+∠ECD=90°,
∴∠ECD+∠CDF=90°,
∴∠CGD=90°,
∴CE⊥DF,故①正確;
在Rt△CGD中,H是CD邊的中點,
∴HG=![]() CD=
CD=![]() AD,故④錯誤;
AD,故④錯誤;
連接AH,如圖:
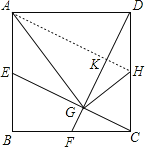
同理可證得:AH⊥DF,
∵HG=HD=![]() CD,
CD,
∴DK=GK,
∴AH垂直平分DG,
∴AG=AD,GH=DH,故②正確;
∴∠DAG=2∠DAH,
在△ADH與△CDF中,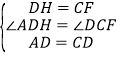 ,
,
∴△ADH≌△DCF,
∴∠DAH=∠CDF,
∵GH=DH,
∴∠HDG=∠HGD,
∴∠GHC=∠HDG+∠HGD=2∠CDF,
又∵AH垂直平分DG,
∴∠DAH=∠GAH,∠DAG=2∠DAH,
∴∠CHG=∠DAG.故③正確;
故選:C.


科目:初中數學 來源: 題型:
【題目】10袋小麥稱重后記錄如下(單位:kg).88.8,91,91.5,89,91.2,91.3,88.9,91.2,91,91.1.
(1)如果每袋小麥以90 kg為標準,超過的千克數記作正數,不足的千克數記作負數,這10袋小麥總計超過多少千克或不足多少千克?
(2)10袋小麥一共多少千克?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】5月23、24日,蘭州市九年級學生進行了中考體育測試,某校抽取了部分學生的一分鐘跳繩測試成績,將測試成績整理后作出如統計圖.甲同學計算出前兩組的頻率和是0.12,乙同學計算出第一組的頻率為0.04,丙同學計算出從左至右第二、三、四組的頻數比為4:17:15.結合統計圖回答下列問題:
(1)這次共抽取了多少名學生的一分鐘跳繩測試成績?
(2)若跳繩次數不少于130次為優秀,則這次測試成績的優秀率是多少?
(3)如果這次測試成績中的中位數是120次,那么這次測試中,成績為120次的學生至少有多少人?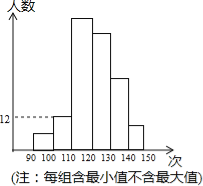
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】企業舉行“愛心一日捐”活動,捐款金額分為五個檔次,分別是50元,100元,150元,200元,300元.宣傳小組隨機抽取部分捐款職工并統計了他們的捐款金額,繪制成兩個不完整的統計圖,請結合圖表中的信息解答下列問題:
(1)宣傳小組抽取的捐款人數為_____人,請補全條形統計圖;
(2)在扇形統計圖中,求100元所對應扇形的圓心角的度數;
(3)已知該企業共有500人參與本次捐款,請你估計捐款總額大約為多少元?

查看答案和解析>>
科目:初中數學 來源: 題型:
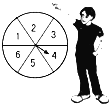
【題目】如圖所示,轉盤被等分成六個扇形,并在上面一次寫上數字1、2、3、4、5、6;若自由轉動轉盤,當它停止轉動時,求:
(1)指針指向4的概率;
(2)指針指向數字是奇數的概率;
(3)指針指向數字不小于5的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】因為sin30°=![]() ,sin210°=
,sin210°=![]() ,所以sin210°=sin(180°+30°)=﹣sin30°;因為sin45°=
,所以sin210°=sin(180°+30°)=﹣sin30°;因為sin45°=![]() ,sin225°=
,sin225°=![]() ,所以sin225°=sin(180°+45°)=﹣sin45°,由此猜想,推理知:一般地當α為銳角時有sin(180°+α)=﹣sinα,由此可知:sin240°=( )
,所以sin225°=sin(180°+45°)=﹣sin45°,由此猜想,推理知:一般地當α為銳角時有sin(180°+α)=﹣sinα,由此可知:sin240°=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料并解決有關問題:
我們知道:|x|=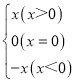 ,現在我們可以用這一結論來化簡含有絕對值的代數式,如化簡代數式|x+1|+|x﹣2|時,可令x+1=0和x﹣2=0,分別求得x=﹣1,x=2(稱﹣1,2分別為|x+1|與|x﹣2|的零點值).在實數范圍內,零點值x=﹣1和x=2可將全體實數分成不重復且不遺漏的如下3種情況:①x<﹣1;②﹣1≤x<2;③x≥2.
,現在我們可以用這一結論來化簡含有絕對值的代數式,如化簡代數式|x+1|+|x﹣2|時,可令x+1=0和x﹣2=0,分別求得x=﹣1,x=2(稱﹣1,2分別為|x+1|與|x﹣2|的零點值).在實數范圍內,零點值x=﹣1和x=2可將全體實數分成不重復且不遺漏的如下3種情況:①x<﹣1;②﹣1≤x<2;③x≥2.
從而化簡代數式|x+1|+|x﹣2|可分以下3種情況:
①當x<﹣1時,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
②當﹣1≤x<2時,原式=x+1﹣(x﹣2)=3;
③當x≥2時,原式=x+1+x﹣2=2x﹣1;
綜上討論,原式=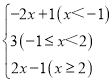
通過以上閱讀,請你解決以下問題:
(1)當x<2時,|x﹣2|= ;
(2)根據材料中的方法化簡代數式|x+2|+|x﹣4|;(寫出解答過程)
(3)直接寫出|x﹣1|﹣4|x+1|的最大值 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=∠ACB,以AC為直徑的⊙O分別交AB、BC于點M、N,點P在AB的延長線上,且∠CAB=2∠BCP.
(1)求證:直線CP是⊙O的切線.
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求點B到AC的距離.
,求點B到AC的距離.
(3)在第(2)的條件下,求△ACP的周長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了更好的治理西流湖水質,保護環境,市治污公司決定購買 10 臺污水處理設備.現有 A、B 兩種型號的設備,其中每臺的價格,月處理污水量如下表:
A 型 | B 型 | |
價格(萬元/臺) | a | b |
處理污水量(噸/月) | 240 | 200 |
經調查:購買一臺 A 型設備比購買一臺 B 型設備多 2 萬元,購買 2 臺 A 型設備比購買 3 臺 B 型設備少 6 萬元.
(1)求 a,b 的值;
(2)經預算:市治污公司購買污水處理設備的資金不超過 105 萬元,你認為該公司 有哪幾種購買方案;
(3)在(2)問的條件下,若每月要求處理西流湖的污水量不低于 2040 噸,為了節 約資金,請你為治污公司設計一種最省錢的購買方案.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com