
【題目】某校為了解本校學生每周參加課外輔導班的情況,隨機調査了部分學生一周內參加課外輔導班的學科數,并將調查結果繪制成如圖1、圖2所示的兩幅不完整統計圖(其中A:0個學科,B:1個學科,C:2個學科,D:3個學科,E:4個學科或以上),請根據統計圖中的信息,解答下列問題:
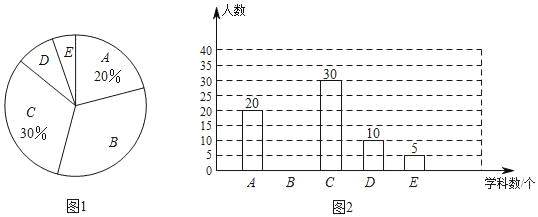
(1)請將圖2的統計圖補充完整;
(2)根據本次調查的數據,每周參加課外輔導班的學科數的眾數是 個學科;
(3)若該校共有2000名學生,根據以上調查結果估計該校全體學生一周內參加課外輔導班在3個學科(含3個學科)以上的學生共有 人.
【答案】(1)圖形見解析;(2)1;(3)300.
【解析】
(1)由A的人數及其所占百分比求得總人數,總人數減去其它類別人數求得B的人數即可補全圖形;
(2)根據眾數的定義求解可得;
(3)用總人數乘以樣本中D和E人數占總人數的比例即可得.
解:(1)∵被調查的總人數為20÷20%=100(人),
則輔導1個學科(B類別)的人數為100﹣(20+30+10+5)=35(人),
補全圖形如下:
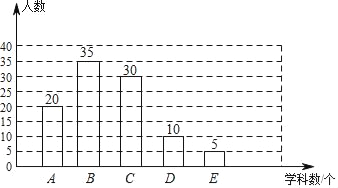
(2)根據本次調查的數據,每周參加課外輔導班的學科數的眾數是1個學科,
故答案為1;
(3)估計該校全體學生一周內參加課外輔導班在3個學科(含3個學科)以上的學生共有2000×![]() =300(人),
=300(人),
故答案為300.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源: 題型:
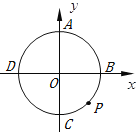
【題目】如圖,半徑為![]() 且坐標原點為圓心的圓交
且坐標原點為圓心的圓交![]() 軸、
軸、![]() 軸于點
軸于點![]() 、
、![]() 、
、![]() 、
、![]() ,過圓上的一動點
,過圓上的一動點![]() (不與
(不與![]() 重合)作
重合)作![]() ,且
,且![]() (
(![]() 在
在![]()
![]() 右側)
右側)
(1)連結![]() ,當
,當![]() 時,則點
時,則點![]() 的橫坐標是______.
的橫坐標是______.
(2)連結![]() ,設線段
,設線段![]() 的長為
的長為![]() ,則
,則![]() 的取值范圍是____.
的取值范圍是____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖①,在等腰直角![]() 中,斜邊
中,斜邊![]() .
.

(1)請你在圖①的![]() 邊上求作一點
邊上求作一點![]() ,使得
,使得![]() ;
;
(2)如圖②,在(1)問的條件下,將![]() 邊沿
邊沿![]() 方向平移,使得點
方向平移,使得點![]() 、
、![]() 、
、![]() 對應點分別為
對應點分別為![]() 、
、![]() 、
、![]() ,連接
,連接![]() ,
,![]() .若平移的距離為1,求
.若平移的距離為1,求![]() 的大小及此時四邊形
的大小及此時四邊形![]() 的面積;
的面積;
(3)將![]() 邊沿
邊沿![]() 方向平移
方向平移![]() 個單位至
個單位至![]() ,是否存在這樣的
,是否存在這樣的![]() ,使得在直線
,使得在直線![]() 上有一點
上有一點![]() ,滿足
,滿足![]() ,且此時四邊形
,且此時四邊形![]() 的面積最大?若存在,求出四邊形
的面積最大?若存在,求出四邊形![]() 面積的最大值及平移距離
面積的最大值及平移距離![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】利用如圖1的二維碼可以進行身份識別.某校建立了一個身份識別系統,圖2是某個學生的識別圖案,黑色小正方形表示1,白色小正方形表示0.將第一行數字從左到右依次記為![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以轉換為該生所在班級序號,其序號為
,那么可以轉換為該生所在班級序號,其序號為![]() .如圖2第一行數字從左到右依次為0,1,0,1,序號為
.如圖2第一行數字從左到右依次為0,1,0,1,序號為![]() ,表示該生為5班學生.表示6班學生的識別圖案是( )
,表示該生為5班學生.表示6班學生的識別圖案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AB=5,過點B作BD⊥AB,點C,D都在AB上方,AD交△BCD的外接圓⊙O于點E.
(1)求證:∠CAB=∠AEC.
(2)若BC=3.
①EC∥BD,求AE的長.
②若△BDC為直角三角形,求所有滿足條件的BD的長.
(3)若BC=EC=![]()
![]() ,則
,則![]() = .(直接寫出結果即可)
= .(直接寫出結果即可)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】深圳天虹某商場從廠家批發電視機進行零售,批發價格與零售價格如下表:
電視機型號 | 甲 | 乙 |
批發價(元/臺) | 1500 | 2500 |
零售價(元/臺) | 2025 | 3640 |
若商場購進甲、乙兩種型號的電視機共50臺,用去9萬元.
(1)求商場購進甲、乙型號的電視機各多少臺?
(2)迎“元旦”商場決定進行優惠促銷:以零售價的七五折銷售乙種型號電視機,兩種電視機銷售完畢,商場共獲利8.5%,求甲種型號電視機打幾折銷售?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是某小區入口抽象成的平面示意圖,已知入口BC寬4米,欄桿支點O與地面BC的距離為0.8米,當欄桿OM升起到與門衛室外墻AB的夾角成30°時,一輛寬2.4米,高1.6米的轎車能否從該入口的正中間位置進入該小區?若能,請通過計算說明;若不能,請說明理由.(參考數據:![]() 1.7)
1.7)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,點D在BC上,BD=DC,過點D作DE⊥AC,垂足為E,⊙O經過A,B,D三點.
(1)求證:AB是⊙O的直徑;
(2)判斷DE與⊙O的位置關系,并加以證明;
(3)若⊙O的半徑為3,∠BAC=60°,求DE的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com