
已知平面直角坐標系中兩定點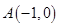 、
、 ,拋物線
,拋物線 過點A,B,與y交于C點,點P(m,n)為拋物線上一點.
過點A,B,與y交于C點,點P(m,n)為拋物線上一點.
(1)求拋物線的解析式和點C的坐標;
(2)當∠APB為鈍角時,求m的取值范圍;
(3)當∠PAB=∠ABC時,求點P的坐標.
解:(1)∵拋物線 過點A,B,
過點A,B,
∴ ,解得:
,解得: ,
,
∴拋物線的解析式為: .
.
∴C .
.
(2)以AB為直徑作圓M,與y軸交于點P.則拋物線在圓內的部分,能使∠APB為鈍角,
∴M( ,0),⊙M的半徑=
,0),⊙M的半徑= .
.
∵P是拋物線與y軸的交點,
∴OP=2,
∴MP= 
∴P在⊙M上,
∴由拋物線的對稱性可知, ,
,
∴當-1<m<0或3<m<4時,∠APB為鈍角.
(3)在Rt△OBC中, .
.
第一種情況:過A作AP∥BC,交拋物線于點P .
∴∠PAB=∠ABC.
過P作PQ⊥AB于Q,
∴ .
.
∵P(m,n),
∴PQ=n,AQ=m+1
∴ .
.
∴ .
.
解得
∴
第二種情況:點P關于x軸的對稱點的坐標為
∴直線AP″的解析式為
∴ 解得
解得
∴
∴
解析試題分析:(1)將A點,B點坐標代入解析式,即可求出解析式,可得 C點坐標;(2)以AB為直徑作圓M,與y軸交于點P.因為AB為直徑,所以當拋物線上的點P在⊙C的內部時,滿足∠APB為鈍角,根據題意可證得P在⊙M上,由拋物線的對稱性可知, ,可得-1<m<0,或3<m<4;(3)根據題意分兩種情況進行討論,即可得出答案.
,可得-1<m<0,或3<m<4;(3)根據題意分兩種情況進行討論,即可得出答案.
考點:二次函數綜合題.
點評:本題是二次函數的綜合題,解答本題的關鍵是熟練掌握待定系數法求二次函數解析式,學生還要熟練掌握數形結合思想、分類討論思想的綜合應用.本題綜合性強,有一定的難度.


 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:初中數學 來源: 題型:填空題
如圖,反映的過程是:曉明從家跑步到體育館,在那里鍛煉了一陣后又走到新華書店去買書,然后散步走回家.其中 表示時間(分鐘),
表示時間(分鐘), 表示曉明離家的距離(千米),那么曉明在體育館鍛煉和在新華書店買書共用去時間是_______________分鐘.
表示曉明離家的距離(千米),那么曉明在體育館鍛煉和在新華書店買書共用去時間是_______________分鐘.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
(本題7分)如圖, 分別表示A步行與B騎車在同一路上行駛的路程S與時間t的關系。
分別表示A步行與B騎車在同一路上行駛的路程S與時間t的關系。
(1)B出發時與A相距 千米。
(2)走了一段路后,自行車發生故障,進行修理,所用的時間是 小時。
(3)B出發后 小時與A相遇。
(4)若B的自行車不發生故障,保持出發時的速度前進, 小時與A相遇?相遇點離B的出發點 千米?在圖中表示出這個相遇點C。
(5)A行走的路程S與時間t的函數關系式為 。
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
下表給出了代數式 與
與 的一些對應值:
的一些對應值:
 | …… | -2 | -1 | 0 | 1 | 2 | 3 | …… |
 | …… | 5 |  | c | 2 | -3 | -10 | …… |
 ,
, ,
, 的值;
的值; ,直接寫出
,直接寫出 時
時 的最大值.
的最大值.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知:如圖,拋物線 與
與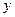 軸交于點
軸交于點 ,與
,與 軸交于
軸交于 、
、 兩點,點
兩點,點 的坐標為
的坐標為 .
.
(1)求拋物線的解析式及頂點 的坐標;
的坐標;
(2)設點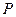 是在第一象限內拋物線上的一個動點,求使與四邊形
是在第一象限內拋物線上的一個動點,求使與四邊形 面積相等的四邊形
面積相等的四邊形 的點
的點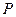 的坐標;
的坐標;
(3)求 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
為支援貧困地區學生,學校開展捐書活動,以下是某學習小組5名學生捐書的冊數:3,9,3,7,8,則這組數據的中位數是 ( )
| A.3 | B.7 | C.8 | D.9 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com