
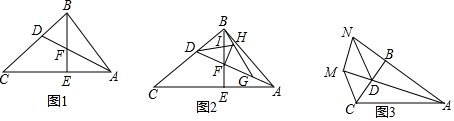
分析 (1)首先證明BD=BF,在Rt△在Rt△ABD中,根據AB=$\sqrt{A{D}^{2}-B{D}^{2}}$計算即可.
(2)如圖2中,作BK∥DG交DH的延長線于K,連接KG.首先證明四邊形BFGK是平行四邊形,再證明IF是△DKG的中位線,由此即可證明.
(3)如圖3中,作MK⊥AC于K,MF⊥BC于K,ME⊥AN于E.首先證明△MFD≌△MEN,推出MN=MD,推出∠MDN=45°,由∠BDA=75°,推出∠NDB=180°-45°-75°=60°,設BD=a.則DN=2a,在AB上取一點P,使得PD=PA,則∠DPB=30°,PD=PA=2a,BP=$\sqrt{3}$a,可得AB=(2+$\sqrt{3}$)a,由此即可解決問題.
解答 (1)解:如圖1中,
∵BE⊥AC,
∴∠BEC=∠ABC=90°,
∴∠C+∠CBE=90°,∠ABE+∠CBE=90°,
∴∠C=∠ABE,
∵AD平分∠BAC,
∴∠DAB=∠DAC,
∵∠BDF=∠C+∠DAC,∠BFD=∠DAB+∠ABE,
∴BD=BF=2$\sqrt{3}$,
在Rt△ABD中,AB=$\sqrt{A{D}^{2}-B{D}^{2}}$=$\sqrt{{6}^{2}-(2\sqrt{3})^{2}}$=2$\sqrt{6}$.
(2)證明:如圖2中,作BK∥DG交DH的延長線于K,連接KG.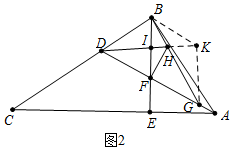
∵FH垂直平分DG,
∴HD=HG,
∴∠HDG=∠HGD,
∴∠HBK=∠HGD,∠HKB=∠HDG,
∴∠HBK=∠HKB,
∴BH=HK,∵∠DHB=∠KHG,
∴△BDH≌△KGH,
∴BD=KG,∵DG=GD,DK=BG,
∴△BDG≌△KGD,
∴∠BDG=∠KGD,
∵∠BDF=∠BFD,
∴∠BFD=∠KGD,
∴BF∥KG,∵BK∥FG,'
∴四邊形BFGK是平行四邊形,
∴BF=GK=BD,
∵DF=FG,FI∥GK,
∴DI=IK,
∴GK=2IF,
∴BD=2IF.
(3)解:結論:∴$\frac{AB}{DN}$=$\frac{2+\sqrt{3}}{2}$.理由如下,
如圖3中,作MK⊥AC于K,MF⊥BC于K,ME⊥AN于E.
∵∠MAE=∠MAK,
∴ME=MK,
∵∠MCK=∠MCB=60°,
∴MK=MF,
∴ME=MF,
∴∠MBE=∠MBF=45°,
∵∠NMD=∠EEMF=90°,
∴∠NME=∠DMF,∵∠MFD=∠MEN,ME=MF,
∴△MFD≌△MEN,
∴MN=MD,
∴∠MDN=45°,
∵∠BDA=75°,
∴∠NDB=180°-45°-75°=60°,設BD=a.則DN=2a,
在AB上取一點P,使得PD=PA,則∠DPB=30°,PD=PA=2a,BP=$\sqrt{3}$a,
∴AB=(2+$\sqrt{3}$)a,
∴$\frac{AB}{DN}$=$\frac{(2+\sqrt{3})a}{2a}$=$\frac{2+\sqrt{3}}{2}$.
點評 本題考查三角形綜合題、全等三角形的判定和性質、平行四邊形的判定和性質、等腰直角三角形的判定和性質,直角三角形30度角性質等知識,解題的關鍵是靈活運用所學知識解決問題,學會添加常用輔助線,構造全等三角形解決問題,學會用轉化的首先思考問題,屬于中考壓軸題.


科目:初中數學 來源: 題型:解答題
| 一戶居民一個月用水量即為x米3 | 水費單價 (單位:元/米3) |
| x≤22 | a |
| 超出22米3的部分 | a+1.1 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖△ABC,AB=AC=24厘米,∠B=∠C,BC=16厘米,點D為AB的中點.點P在線段BC上以4厘米/秒的速度由B點向C點運動,同時,點Q在線段CA上由C點向A點運動.若點Q的運動速度為v厘米/秒,則當△BPD與△CQP全等時,v的值為4或6 厘米/秒.
如圖△ABC,AB=AC=24厘米,∠B=∠C,BC=16厘米,點D為AB的中點.點P在線段BC上以4厘米/秒的速度由B點向C點運動,同時,點Q在線段CA上由C點向A點運動.若點Q的運動速度為v厘米/秒,則當△BPD與△CQP全等時,v的值為4或6 厘米/秒.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,?ABCD對角線AC、BD相交于點O,E,F分別是OA,OC的中點,連接BE,DF.
如圖,?ABCD對角線AC、BD相交于點O,E,F分別是OA,OC的中點,連接BE,DF.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
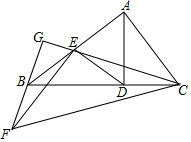 如圖,Rt△ABC中,∠BAC=90°,過點A作AD⊥BC于點D,點E為線段AB中點,連接ED,EC將△EDC繞點E旋轉,使點D和點B重合,得到△EBF,延長FB、CE相交于點G,若BC=$\sqrt{5}$,則BG=$\frac{\sqrt{5}}{3}$.
如圖,Rt△ABC中,∠BAC=90°,過點A作AD⊥BC于點D,點E為線段AB中點,連接ED,EC將△EDC繞點E旋轉,使點D和點B重合,得到△EBF,延長FB、CE相交于點G,若BC=$\sqrt{5}$,則BG=$\frac{\sqrt{5}}{3}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com