
(12分)已知,平面直角坐標系中,矩形OABC的邊OC在x軸正半軸上,邊OA在y軸正半軸上,B點的坐標為(4,3).將△AOC沿對角線AC所在的直線翻折,得到△AO’C,點O’為點O的對稱點,CO’與AB相交于點E(如圖①).
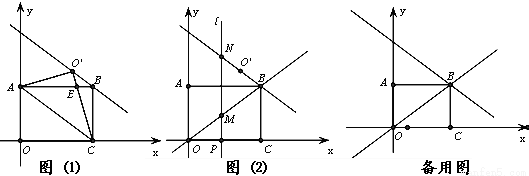
(1)試說明:EA=EC;
(2)求直線BO’的解析式;
(3)作直線OB(如圖②),直線l平行于y軸,分別交x軸、直線OB、O’B于點P、M、N,設P點的橫坐標為m (m>0)。y軸上是否存在點F,使得ΔFMN為等腰直角三角形?若存在,請求出此時m的值;若不存在,請說明理由.
(1)見解析; (2)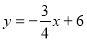 (3)
(3)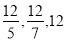
【解析】
試題分析:(1)要想證EA=EC,只需要證∠EAC=∠ACE即可,而由折疊的性質可得∠ACO=∠ACE,再根據矩形的性質可得∠EAC=∠ACO,可證;(2)先求得點O’的坐標,然后用待定系數法求函數解析式即可;
(3)用P點的橫坐標為m表示出點M、N的坐標及線段MN的長度,然后分情況討論解答即可.
試題解析:(1)由折疊得∠ACO=∠ACE,∵四邊形OABC是矩形,∴AB∥CO,∴∠EAC=∠ACO,∴∠EAC=∠ACE,∴EA=EC;
(2)由題意得點O’的坐標為(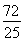 ,
,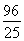 ),設函數關系式為
),設函數關系式為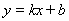
∵圖象過點(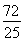 ,
,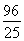 ),(4,3)
),(4,3)
 ,解得
,解得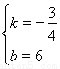
∴函數關系式為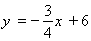 ①;
①;
(3)∵B為(4,3),所以直線BO為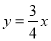 ②,∵l∥y軸,交x軸于P,P點的橫坐標為m,∴P(m,0)(m>0),∴直線l的解析式為x=m③,解②③得M(m,
②,∵l∥y軸,交x軸于P,P點的橫坐標為m,∴P(m,0)(m>0),∴直線l的解析式為x=m③,解②③得M(m,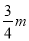 );解①②得:N(m,-
);解①②得:N(m,- 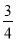 m+6),∴MN=|-
m+6),∴MN=|-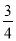 m+6|,Ⅰ)當∠FMN=90°且△FMN為等腰三角形時,F(0,
m+6|,Ⅰ)當∠FMN=90°且△FMN為等腰三角形時,F(0,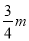 ),∴FM=MN,即:m=|-
),∴FM=MN,即:m=|- 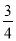 m+6|,解得:m=
m+6|,解得:m=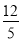 或m=12,Ⅱ)同理當∠FNM=90°且△FMN為等腰三角形時,F(0,-
或m=12,Ⅱ)同理當∠FNM=90°且△FMN為等腰三角形時,F(0,- 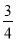 m+6),∴FN=MN,即:m=|-
m+6),∴FN=MN,即:m=|-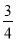 m+6|,解得:m=
m+6|,解得:m= 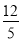 或m=12,Ⅲ)當∠MFN=90°且△FMN為等腰三角形時,F(0,3),∴
或m=12,Ⅲ)當∠MFN=90°且△FMN為等腰三角形時,F(0,3),∴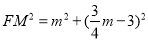 ,
,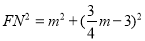 ,
,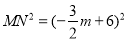 ,而
,而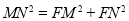 ,所以
,所以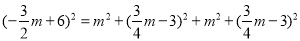 ,解得m=
,解得m=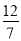 或m=-12(舍去);綜上可知存在使得△FMN為等腰直角三角形的點F,此時m的值為
或m=-12(舍去);綜上可知存在使得△FMN為等腰直角三角形的點F,此時m的值為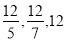 .
.
考點:1.待定系數法求函數解析式;2.等腰三角形的判定;3.折疊的性質;4.勾股定理.


 課課優能力培優100分系列答案
課課優能力培優100分系列答案 優百分課時互動系列答案
優百分課時互動系列答案科目:初中數學 來源:2014-2015學年江蘇省鹽城市阜寧縣九年級上學期期中學情調研數學試卷(解析版) 題型:填空題
如圖,⊙O的內接四邊形ABCD中,∠BCD=138°,則∠BOD的度數是 .
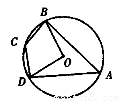
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省興化顧莊等三校九年級上學期12月月考數學試卷(解析版) 題型:選擇題
若如圖所示的兩個四邊形相似,則∠α的度數是 ( )

A.870 B.600 C.750 D.1200
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省九年級上學期第三次教學質量監測數學試卷(解析版) 題型:選擇題
甲、乙、丙三名射擊運動員在某場測試中各射擊10次,3人的測試成績如下表

則甲、乙、丙3名運動員測試成績最穩定的是 ( )
A.甲 B.乙 C.丙 D.3人成績穩定情況相同
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省興化顧莊三校八年級上學期12月月考數學試卷(解析版) 題型:解答題
(10分)如圖,直線l1的解析式為y=-x+2,l1與x軸交于點B,直線l2經過點D(0,5),與直
線l1交于點C(-1,m),且與x軸交于點A

(1)求點C的坐標及直線l2的解析式;(2)求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省七年級上學期期中考試數學試卷(解析版) 題型:解答題
(本題5分)定義一種新運算:觀察下列各式:
1⊙3=1×4+3=7 ;3⊙(-1)= 3×4-1=11;5⊙4=5×4+4=24 ;4⊙(-3)= 4×4-3=13
(1)請你想一想:a⊙b=___________;
(2)若a≠b,那么a⊙b______b⊙a(填入 “=”或 “≠ ”) ;
(3)若a⊙(-2b) = 4,請計算 (a-b)⊙(2a+b)的值.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省八年級上學期第二次月考數學試卷(解析版) 題型:選擇題
如圖,是張老師出門散步時離家的距離 與時間
與時間 之間的函數關系的圖象,若用黑點表示張老師家的位置,則張老師散步行走的路線可能是( )
之間的函數關系的圖象,若用黑點表示張老師家的位置,則張老師散步行走的路線可能是( )


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com