
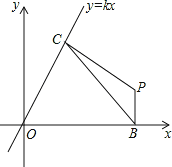
【題目】如圖,已知平面直角坐標系中,直線y=kx(k≠0)經過點(a,![]() a)(a>0).線段BC的兩個端點分別在x軸與直線y=kx上(B、C均與原點O不重合)滑動,且BC=2,分別作BP⊥x軸,CP⊥直線y=kx,交點為P,經探究在整個滑動過程中,P、O兩點間的距離為定值 .
a)(a>0).線段BC的兩個端點分別在x軸與直線y=kx上(B、C均與原點O不重合)滑動,且BC=2,分別作BP⊥x軸,CP⊥直線y=kx,交點為P,經探究在整個滑動過程中,P、O兩點間的距離為定值 .
【答案】![]() .
.
【解析】
試題解析:∵直線y=kx(k≠0)經過點(a,![]() a),
a),
∴tan∠COB=![]() ,
,
∴∠COB=60°,
過點C作CE⊥x軸于點E,延長CP交x軸于點F,連接OP,如圖,
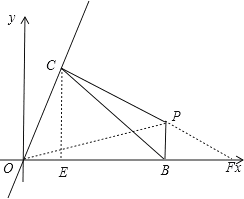
則∠OCE=∠CFE=30°,
設P點坐標為(x,y)(不妨設點P在第一象限,其他同理可求得),則OB=x,PB=y,
在Rt△PBF中,可得BF=![]() y,
y,
∴OF=OB+BF=x+![]() y,
y,
在Rt△OCF中,OC=![]() OF=
OF=![]() ,
,
在Rt△OCE中,OE=![]() OC=
OC=![]() ,
,
則CE=![]() OE=
OE=![]() ,BE=OB-OE=x-
,BE=OB-OE=x-![]() =
=![]() ,
,
在Rt△BCE中,由勾股定理可得CE2+BE2=BC2,
∴(![]() )2+(
)2+(![]() )2=22,
)2=22,
整理可求得x2+y2=![]() ,
,
∴OP=![]() ,
,
即O、P兩點的距離為定值![]()


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:初中數學 來源: 題型:
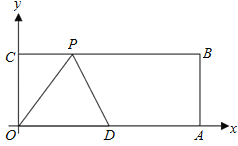
【題目】如圖,在平面直角坐標系中,矩形OABC的頂點A、C的坐標分別為(10,0),(0,4),點D是OA的中點,點P在BC上運動,當ΔODP是腰長為5的等腰三角形時,點P的坐標為___________
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com