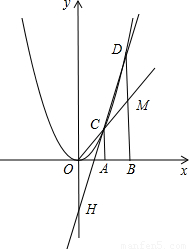
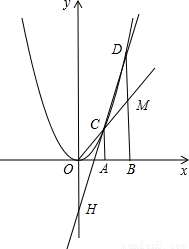
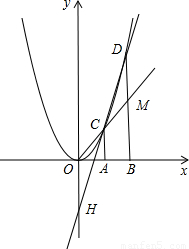
解:(1)由已知可得點B的坐標為(2,0),點C坐標為(1,1),點D的坐標為(2,4),
由點C坐標為(1,1)易得直線OC的函數解析式為y=x,
故點M的坐標為(2,2),
所以S
△CMD=1,S
梯形ABMC=

所以S
△CMD:S
梯形ABMC=2:3,
即結論①成立.
設直線CD的函數解析式為y=kx+b,
則
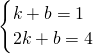
,
解得
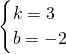
所以直線CD的函數解析式為y=3x-2.
由上述可得,點H的坐標為(0,-2),y
H=-2
因為x
C•x
D=2,
所以x
C•x
D=-y
H,
即結論②成立;
(2)(1)的結論仍然成立.
理由:當A的坐標(t,0)(t>0)時,點B的坐標為(2t,0),點C坐標為(t,t2),點D的坐標為(2t,4t2),
由點C坐標為(t,t2)易得直線OC的函數解析式為y=tx,
故點M的坐標為(2t,2t2),
所以S
△CMD=t3,S
梯形ABMC=

t3.
所以S
△CMD:S
梯形ABMC=2:3,
即結論①成立.
設直線CD的函數解析式為y=kx+b,
則
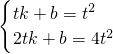
,
解得

所以直線CD的函數解析式為y=3tx-2t
2;
由上述可得,點H的坐標為(0,-2t2),y
H=-2t
2因為x
C•x
D=2t
2,
所以x
C•x
D=-y
H,
即結論②成立;
(3)由題意,當二次函數的解析式為y=ax
2(a>0),且點A坐標為(t,0)(t>0)時,點C坐標為(t,at
2),點D坐標為(2t,4at
2),
設直線CD的解析式為y=kx+b,
則:

,
解得
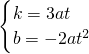
所以直線CD的函數解析式為y=3atx-2at
2,則點H的坐標為(0,-2at
2),y
H=-2at
2.
因為x
C•x
D=2t
2,
所以x
C•x
D=-

y
H.
分析:(1)可先根據AB=OA得出B點的坐標,然后根據拋物線的解析式和A,B的坐標得出C,D兩點的坐標,再依據C點的坐標求出直線OC的解析式.進而可求出M點的坐標,然后根據C、D兩點的坐標求出直線CD的解析式進而求出D點的坐標,然后可根據這些點的坐標進行求解即可;
(2)(3)的解法同(1)完全一樣.
點評:本題主要考查了二次函數的應用、一次函數解析式的確定、圖形面積的求法、函數圖象的交點等知識點.

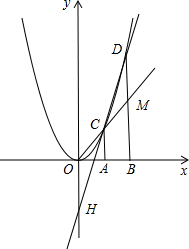 線OC交BD于點M,直線CD交y軸于點H,記點C、D的橫坐標分別為xC、xD,點H的縱坐標為yH.
線OC交BD于點M,直線CD交y軸于點H,記點C、D的橫坐標分別為xC、xD,點H的縱坐標為yH.
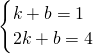 ,
,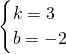
 t3.
t3.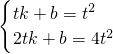 ,
,
 ,
,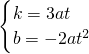
 yH.
yH.

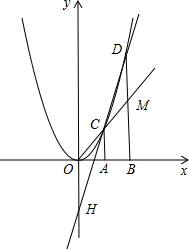 線OC交BD于點M,直線CD交y軸于點H,記點C、D的橫坐標分別為xC、xD,點H的縱坐標為yH.
線OC交BD于點M,直線CD交y軸于點H,記點C、D的橫坐標分別為xC、xD,點H的縱坐標為yH.