
將點A(0,2)繞著原點O順時針方向旋轉45°角到對應點A′,則點A′的坐標是 .
(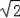
 ,
,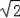
 ) .
) .
【考點】坐標與圖形變化-旋轉.
【專題】計算題.
【分析】如圖,作A′H⊥OA于H,根據旋轉的性質得OA′=OA=2,∠AOA′=45°,則可判斷△OAA′為等腰直角三角形,所以OH=A′H=
 OA′=
OA′=
 ,然后根據第一象限內點的坐標特征寫出點A′的坐標.
,然后根據第一象限內點的坐標特征寫出點A′的坐標.
【解答】解:如圖,作A′H⊥OA于H,
∵點A(0,2)繞著原點O順時針方向旋轉45°角到對應點A′,
∴OA′=OA=2,∠AOA′=45°,
∴△OAA′為等腰直角三角形,
∴OH=A′H=
 OA′=
OA′=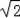
 ,
,
∴點A′的坐標是(
 ,
,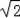
 ).
).
故答案為(
 ,
,
 ).
).


【點評】本題考查了坐標與圖形變化﹣旋轉:圖形或點旋轉之后要結合旋轉的角度和圖形的特殊性質來求出旋轉后的點的坐標.常見的是旋轉特殊角度如:30°,45°,60°,90°,180°.


科目:初中數學 來源: 題型:
如圖坐標系中,O(0,0) ,A(6,6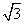 ),B(12,0).將△OAB沿直線CD折疊,使點A
),B(12,0).將△OAB沿直線CD折疊,使點A
恰好落在線段OB上的點E處,若OE=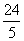 ,則CE : DE的值是 .
,則CE : DE的值是 .
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com