
 ,延長OE到點F,使EF=2OE.
,延長OE到點F,使EF=2OE.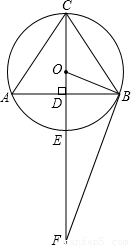
 ,在Rt△BOD中,設OD=x,則OB=3x,利用勾股定理可計算出x=
,在Rt△BOD中,設OD=x,則OB=3x,利用勾股定理可計算出x= ,則OB=3x=
,則OB=3x= ;
; ,則
,則 =
= ,而
,而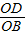 =
= ,于是得到
,于是得到 =
= ,根據(jù)相似三角形的判定即可得到△OBF∽△ODB,根據(jù)相似三角形的性質(zhì)有∠OBF=∠ODB=90°,然后根據(jù)切線的判定定理即可得到結(jié)論.
,根據(jù)相似三角形的判定即可得到△OBF∽△ODB,根據(jù)相似三角形的性質(zhì)有∠OBF=∠ODB=90°,然后根據(jù)切線的判定定理即可得到結(jié)論.
 ,
, ,
, ,
, ,
, ;
; ,
, =
= ,
, =
= ,
, =
= ,
,

湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com