www.黄色片视频,成人av网站免费观看,中文亚洲欧美

<tfoot id="80okg"></tfoot>

<fieldset id="80okg"></fieldset>

<ul id="80okg"></ul>

精英家教網 > 初中數學 > 題目詳情

如圖六邊形ABCDEF是軸對稱圖形，CF所在的直線是它的對稱軸，若∠AFC＋∠BCF＝15°，則∠AFE＋∠BCD的大小是（）

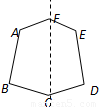
A．150° B．300° C．210° D．330°

【答案】

B．

【解析】

試題分析：因為六邊形ABCDEF是軸對稱圖形，CF所在的直線是它的對稱軸，所以∠AFC=∠EFC，∠BCF=∠DCF，因為∠AFC+∠BCF=150°，所以∠AFE+∠BCD=150°×2=300°．故選B．

考點：軸對稱的性質．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：

（1）已知△ABC為正三角形，點M是射線BC上任意一點，點N是射線CA上任意一點，且BM=CN，直線BN與AM相交于Q點．就下面給出的三種情況（如圖①、②、③），先用量角器分別測量∠BQM的大小，然后猜測∠BQM等于多少度，并利用圖③證明你的結論．

（2）將（1）中的“正△ABC”分別改為正方形ABCD（如圖④）、正五邊形ABCDE（如圖⑤）．正六邊形ABCDEF（如圖③）、…、正n邊形ABCD…X（如圖（n）），“點N是射線CA上任意一點”改為點N是射線CD上任意一點，其余條件不變，根據（1）的求解思路，分別推斷∠BQM各等于多少度，將結論填入下表：

查看答案和解析>>

科目：初中數學 來源： 題型：

（1）如圖，正△ABC中，點M與點N分別是BC、CA上的點，且BM=CN，連接AM、BN，兩線交于點Q，求∠AQN的度數．

（2）將1題中的“正△ABC”分別改為正方形ABCD，正五邊形ABCDE，正六邊形ABCDEF，…，正n邊形ABCD…N，其余條件不變，根據第1題的求解思路分別推斷∠AQN的度數，將結論填入下表：

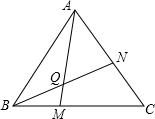
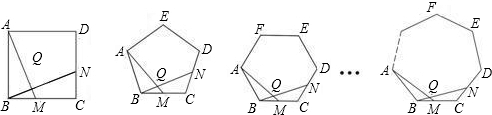
正多邊形	正方形	正五邊形	正六邊形	…	正n邊形
∠AQN的度數

查看答案和解析>>

科目：初中數學 來源： 題型：閱讀理解

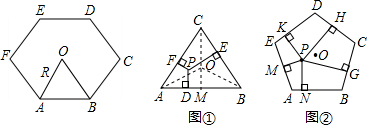（2012•青島模擬）同學們已經認識了很多正多邊形，現以正六邊形為例再介紹與正多邊形相關的幾個概念．如正六邊形ABCDEF各邊對稱軸的交點O，又稱正六邊形的中心，其中OA稱正六邊形的半徑，通常用R表示，∠AOB稱為中心角，顯然．提出問題：正多邊形內任意一點到各邊距離之和與這個正多邊形的半徑R和中心角有什么關系？
探索發現：
（1）為了解決這個問題，我們不妨從最簡單的正多邊形--正三角形入手．
如圖①，△ABC是正三角形，半徑OA=R，∠AOB是中心角，P是△ABC內任意一點，P到△ABC各邊距離分別為h₁、h₂、h₃，確定h₁+h₂+h₃的值與△ABC的半徑R及中心角的關系．
解：設△ABC的邊長是a，面積為S，顯然S=

a（h₁+h₂+h₃）
O為△ABC的中心，連接OA、OB、OC，它們將△ABC分成三個全等的等腰三角形，過點O作OM⊥AB，垂足為M，Rt△AOM中，易知
OM=OAcos∠AOM=Rcos

∠AOB=Rcos

×120°=Rcos60°，
AM=OAsin∠AOM=Rsin

∠AOB=Rsin

×120°=Rcos60°
∴AB=a=2AM=2Rsin60°
∴S_△AOB=

AB×OM=

×2Rsin60°•Rcos60°=R²sin60°cos60°
∴S_△ABC=3S_△AOB=3R²sin60°cos60°
∴

a（h₁+h₂+h₃）=3R²sin60°cos60°
即：

×2Rsin60°（h₁+h₂+h₃）=3R²sin60°cos60°
∴h₁+h₂+h₃=3Rcos60°
（2）如圖②，五邊形ABCDE是正五邊形，半徑是R，P是正五邊形ABCDE內任意一點，P到五邊形ABCDE各邊距離分別為h₁、h₂、h₃、h₄、h₅，參照（1）的探索過程，確定h₁+h₂+h₃+h₄+h₅的值與正五邊形ABCDE的半徑R及中心角的關系．
（3）類比上述探索過程，直接填寫結論
正六邊形（半徑是R）內任意一點P到各邊距離之和 h₁+h₂+h₃+h₄+h₅+h₆=

6Rcos30°

正八邊形（半徑是R）內任意一點P到各邊距離之和 h₁+h₂+h₃+h₄+h₅+h₆+h₇+h₈=

8Rcos22.5°

正n邊形（半徑是R）內任意一點P到各邊距離之和 h₁+h₂+…+h_n=

nRcos

180°

nRcos

180°

．

查看答案和解析>>

科目：初中數學 來源： 題型：

（2013•婺城區一模）某學習小組在探索“各內角都相等的圓內接多邊形是否為正多邊形”時，有如下探討：

甲同學：我發現這種多邊形不一定是正多邊形．如圓內接矩形不一定是正方形．
乙同學：我知道，邊數為3時，它是正三角形；我想，邊數為5時，它可能也是正五邊形…
丙同學：我發現邊數為6時，它也不一定是正六邊形．如圖2，△ABC是正三角形，弧AD、弧BE、弧CF均相等，這樣構造的六邊形ADBECF不是正六邊形．
（1）如圖1，若圓內接五邊形ABCDE的各內角均相等，則∠ABC=

108°

，請簡要說明圓內接五邊形ABCDE為正五邊形的理由．
（2）如圖2，請證明丙同學構造的六邊形各內角相等．
（3）根據以上探索過程，就問題“各內角都相等的圓內接多邊形是否為正多邊形”的結論與“邊數n（n≥3，n為整數）”的關系，提出你的猜想（不需證明）．

查看答案和解析>>

科目：初中數學 來源： 題型：

如圖，四邊形ABCD的內角和為2×180°=360°，五邊形ABCDE的內角和為3×180°=540°，…由此可見：
（1）六邊形的內角和為

720

度；
（2）n邊形的內角和為

（n-2）×180

度．

查看答案和解析>>

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學