
已知拋物線![]() (其中a ≠ c且a ≠0).
(其中a ≠ c且a ≠0).
(1)求此拋物線與x軸的交點坐標;(用a,c的代數式表示)
(2)若經過此拋物線頂點A的直線![]() 與此拋物線的另一個交點為
與此拋物線的另一個交點為![]() ,
,
求此拋物線的解析式;
(3)點P在(2)中x軸上方的拋物線上,直線![]() 與 y軸的交點為C,若
與 y軸的交點為C,若
![]() ,求點P的坐標;
,求點P的坐標;
(4)若(2)中的二次函數的自變量x在n≤x<![]() (n為正整數)的范圍內取值時,記它的整數函數值的個數為N, 則N關于n的函數關系式為 .
(n為正整數)的范圍內取值時,記它的整數函數值的個數為N, 則N關于n的函數關系式為 .
解:(1)拋物線![]() 與x軸交點的橫坐標是關于x的方程
與x軸交點的橫坐標是關于x的方程![]() (其中a ≠ 0,a ≠c)的解.
(其中a ≠ 0,a ≠c)的解.
解得 ![]() ,
,![]() .
.
∴ 拋物線與x軸交點的坐標為![]() ,
,![]() .
.
(2)拋物線![]() 的頂點A的坐標為
的頂點A的坐標為![]() .
.
|
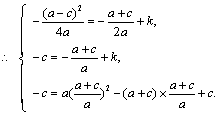
由③得 c =0.
將其代入①、② 得 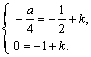
解得 ![]() .
.
 ∴ 所求拋物線的解析式為
∴ 所求拋物線的解析式為 ![]() .
.
(3)作PE⊥x軸于點E, PF⊥y軸于點F.(如圖7)
拋物線![]() 的頂點A的坐標
的頂點A的坐標![]() ,
,
點B的坐標為![]() ,點C的坐標為
,點C的坐標為![]() .
.
設點P的坐標為![]() .
.
∵ 點P在x軸上方的拋物線![]() 上,
上,
∴ ![]() ,且0<m<1,
,且0<m<1,![]() .
.
∴ ![]() ,
,![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
解得 m=2n,或![]() (舍去).
(舍去).
將m=2n代入![]() ,得
,得![]() .
.
解得![]() ,
,![]() (舍去).
(舍去).
∴ ![]() .
.
∴ 點P的坐標為![]() .
.
(4)N關于n的函數關系式為N=4n .
說明:二次函數![]() 的自變量x在n≤x<
的自變量x在n≤x<![]() (n為正整數)的范圍內取值,此時y隨x的增大而減小,
(n為正整數)的范圍內取值,此時y隨x的增大而減小,
∴ ![]() <y≤
<y≤![]() ,
,
其中的整數有![]() ,
,![]() ,…
,…![]() .
.
![]() .
.


 走進文言文系列答案
走進文言文系列答案科目:初中數學 來源: 題型:
已知拋物線![]() (其中a ≠ c且a ≠0).
(其中a ≠ c且a ≠0).
1.(1)求此拋物線與x軸的交點坐標;(用a,c的代數式表示)
2.(2)若經過此拋物線頂點A的直線![]() 與此拋物線的另一個交點為
與此拋物線的另一個交點為![]() ,求此拋物線的解析式;
,求此拋物線的解析式;
3.(3)點P在(2)中x軸上方的拋物線上,直線![]() 與 y軸的交點為C,
與 y軸的交點為C,
若![]() ,求點P的坐標;
,求點P的坐標;
查看答案和解析>>
科目:初中數學 來源: 題型:
已知拋物線![]() (其中
(其中![]() ).
).
1.(1)求該拋物線與x軸的交點坐標及頂點坐標(可以用含k的代數式表示);
2.(2)若記該拋物線的頂點坐標為![]() ,直接寫出
,直接寫出![]() 的最小值;
的最小值;
3.(3)將該拋物線先向右平移![]() 個單位長度,再向上平移
個單位長度,再向上平移![]() 個單位長度,隨著
個單位長度,隨著![]() 的變化,平移后的拋物線的頂點都在某個新函數的圖象上,求這個新函數的解析式(不要求寫自變量的取值范圍).
的變化,平移后的拋物線的頂點都在某個新函數的圖象上,求這個新函數的解析式(不要求寫自變量的取值范圍).
查看答案和解析>>
科目:初中數學 來源: 題型:
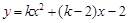 (其中
(其中 ).
).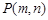 ,直接寫出
,直接寫出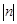 的最小值;
的最小值;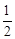 個單位長度,再向上平移
個單位長度,再向上平移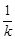 個單位長度,隨著
個單位長度,隨著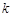 的變化,平移后的拋物線的頂點都在某個新函數的圖象上,求這個新函數的解析式(不要求寫自變量的取值范圍).
的變化,平移后的拋物線的頂點都在某個新函數的圖象上,求這個新函數的解析式(不要求寫自變量的取值范圍).查看答案和解析>>
科目:初中數學 來源:2011-2012年北京宣武外國語實驗學校九年級第一學期期中考試數學卷 題型:解答題
已知拋物線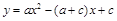 (其中a ≠ c且a ≠0).
(其中a ≠ c且a ≠0).
1.(1)求此拋物線與x軸的交點坐標;(用a,c的代數式表示)
2.(2)若經過此拋物線頂點A的直線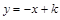 與此拋物線的另一個交點為
與此拋物線的另一個交點為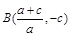 ,求此拋物線的解析式;
,求此拋物線的解析式;
3.(3)點P在(2)中x軸上方的拋物線上,直線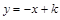 與 y軸的交點為C,
與 y軸的交點為C,
若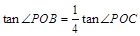 ,求點P的坐標;
,求點P的坐標;
查看答案和解析>>
科目:初中數學 來源:2012屆北京市西城區九年級第一學期期末測試數學卷 題型:解答題
已知拋物線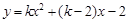 (其中
(其中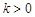 ).
).
1.(1)求該拋物線與x軸的交點坐標及頂點坐標(可以用含k的代數式表示);
2.(2)若記該拋物線的頂點坐標為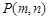 ,直接寫出
,直接寫出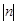 的最小值;
的最小值;
3.(3)將該拋物線先向右平移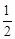 個單位長度,再向上平移
個單位長度,再向上平移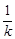 個單位長度,隨著
個單位長度,隨著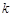 的變化,平移后的拋物線的頂點都在某個新函數的圖象上,求這個新函數的解析式(不要求寫自變量的取值范圍).
的變化,平移后的拋物線的頂點都在某個新函數的圖象上,求這個新函數的解析式(不要求寫自變量的取值范圍).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com