
【題目】已知A(x1,y1),B(x2,y2)是二次函數上y=ax2-2ax+a-c(a≠0)的兩點,若x1≠x2,且y1=y2,則當 自變量x的值取x1+x2時,函數值為( )
A. -cB. cC. -a+cD. a-c
 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線l1的解析式是![]() ,直線l2的解析式是
,直線l2的解析式是![]() ,點A1在l1上,A1的橫坐標為
,點A1在l1上,A1的橫坐標為![]() ,作
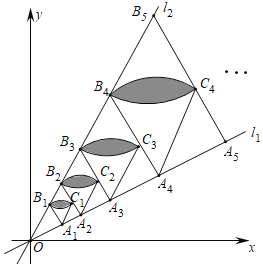
,作![]() 交l2于點B1,點B2在l2上,以B1A1,B1B2為鄰邊在直線l1,l2間作菱形A1B1B2C1,分別以點A1,B2為圓心,以A1B1為半徑畫弧得扇形B1A1C1和扇形B1B2C1,記扇形B1A1C1與扇形B1B2C1重疊部分的面積為S1;延長B2C1交l1于點A2,點B3在l2上,以B2A2,B2B3為鄰邊在l1,l2間作菱形A2B2B3C2,分別以點A2,B3為圓心,以A2B2為半徑畫弧得扇形B2A2C2和扇形B2B3C2,記扇形B2A2C2與扇形B2B3C2重疊部分的面積為S2……按照此規律繼續作下去,則
交l2于點B1,點B2在l2上,以B1A1,B1B2為鄰邊在直線l1,l2間作菱形A1B1B2C1,分別以點A1,B2為圓心,以A1B1為半徑畫弧得扇形B1A1C1和扇形B1B2C1,記扇形B1A1C1與扇形B1B2C1重疊部分的面積為S1;延長B2C1交l1于點A2,點B3在l2上,以B2A2,B2B3為鄰邊在l1,l2間作菱形A2B2B3C2,分別以點A2,B3為圓心,以A2B2為半徑畫弧得扇形B2A2C2和扇形B2B3C2,記扇形B2A2C2與扇形B2B3C2重疊部分的面積為S2……按照此規律繼續作下去,則![]() ________.(用含有正整數n的式子表示)
________.(用含有正整數n的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
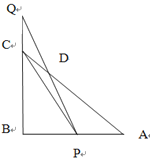
【題目】如圖,等腰Rt△ABC的直角邊AB=2,點P、Q分別從A、C兩點同時出發,以相等的速度作直線運動,已知點P沿射線AB運動,點Q沿邊BC的延長線運動,PQ與直線相交于點D.
(1)設AP的長為x,△PCQ的面積為S,求出S關于x的函數關系式;
(2)當AP的長為何值時,![]() =
=![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某品牌相機,原售價每臺4000元,經連續兩次降價后,現售價每臺3240元,已知兩次降價的百分率一樣。
(1)求每次降價的百分率;
(2)如果按這個百分率再降價一次,求第三次降價后的售價?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀:我們約定,在平面直角坐標系中,經過某點且平行于坐標軸或平行于兩坐標軸夾角平分線的直線,叫該點的“特征線”.例如,點M(1,3)的特征線有:x=1,y=3,y=x+2,y=x+4.如圖,在平面直角坐標系中有正方形OABC,點B在第一象限,A、C分別在x軸和y軸上,拋物線![]() 經過B.C兩點,頂點D在正方形內部.
經過B.C兩點,頂點D在正方形內部.
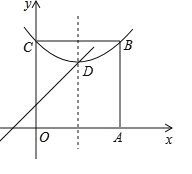
(1)寫出點M(2,3)任意兩條特征線___________________
(2)若點D有一條特征線是y=x+1,求此拋物線的解析式________________________
查看答案和解析>>
科目:初中數學 來源: 題型:
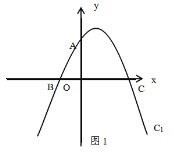
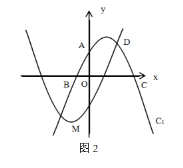
【題目】如圖(1),在平面直角坐標系x Oy中,直線y=2x+4與y軸交于點A,與x軸交于點B,拋物線C1:y=![]() x2+bx+c過A,B兩點,與x軸的另一交點為點C.
x2+bx+c過A,B兩點,與x軸的另一交點為點C.
(1)求拋物線C1的解析式及點C的坐標;
(2)如圖(2),作拋物線C2,使得拋物線C2與C1恰好關于原點對稱,C2與C1在第一象限內交于點D,連接AD,CD,請直接寫出拋物線C2的解析式和點D的坐標.
(3)已知拋物線C2的頂點為M,設P為拋物線C1對稱軸上一點,Q為直線y=2x+4上一點,是否存在以點M,Q,P,B為頂點的四邊形為平行四邊形?若存在,直接寫出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著移動互聯網的快速發展,基于互聯網的共享單車應運而生.為了解某單位使用共享單車的情況,該單位有200名員工,某研究小組隨機采訪10位員工,得到這10位員工一周內使用共享單車的次數分別為:17,12,15,20,17,0,7,26,17,9.
(1)這組數據的中位數是 ,眾數是
(2)試用平均數估計該單位員工一周內使用共享單車的總次數.
查看答案和解析>>
科目:初中數學 來源: 題型:
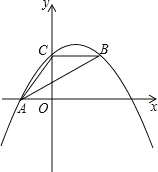
【題目】如圖,拋物線y=ax2+bx+4 經過點A(﹣3,0),點 B 在拋物線上,CB∥x軸,且AB 平分∠CAO.則此拋物線的解析式是___________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com