
【題目】(1)問題背景:如圖1,在四邊形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分別是BC,CD上的點,且∠EAF=60°,請探究圖中線段BE,EF,FD之間的數量關系是什么?
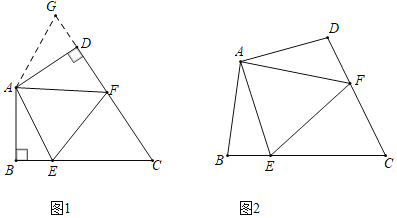
小明探究此問題的方法是:延長FD到點G,使DG=BE,連結AG.先證明△ABE≌△ADG,得AE=AG;再由條件可得∠EAF=∠GAF,證明△AEF≌△AGF,進而可得線段BE,EF,FD之間的數量關系是 .
(2)拓展應用:
如圖2,在四邊形ABCD中,AB=AD,∠B+∠D=180°.E,F分別是BC,CD上的點,且∠EAF=![]() ∠BAD.問(1)中的線段BE,EF,FD之間的數量關系是否還成立?若成立,請給出證明;若不成立,請說明理由.
∠BAD.問(1)中的線段BE,EF,FD之間的數量關系是否還成立?若成立,請給出證明;若不成立,請說明理由.
【答案】(1)EF=BE+DF;(2)結論EF=BE+DF仍然成立;證明見解析.
【解析】
(1)延長FD到點G.使DG=BE.連結AG,即可證明△ABE≌△ADG,可得AE=AG,再證明△AEF≌△AGF,可得EF=FG,即可解題;
(2)延長FD到點G.使DG=BE.連結AG,即可證明△ABE≌△ADG,可得AE=AG,再證明△AEF≌△AGF,可得EF=FG,即可解題.
(1)EF=BE+DF,
理由如下:
在△ABE和△ADG中,
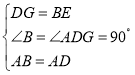 ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
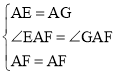 ,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案為:EF=BE+DF.
(2)結論EF=BE+DF仍然成立;
理由:延長FD到點G.使DG=BE.連結AG,如圖2,
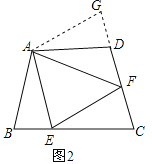
∵∠B+∠ADC=180°,∠ADC+∠ADG=180°,
∴∠B=∠ADG,
在△ABE和△ADG中,
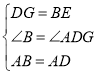 ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
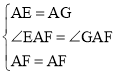 ,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源: 題型:
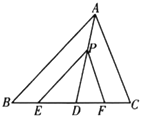
【題目】請在下列橫線上注明理由.
如圖,在![]() 中,點
中,點![]() ,
,![]() ,
,![]() 在邊
在邊![]() 上,點
上,點![]() 在線段
在線段![]() 上,若
上,若![]() ,
,![]() ,點
,點![]() 到
到![]() 和
和![]() 的距離相等.求證:點
的距離相等.求證:點![]() 到
到![]() 和
和![]() 的距離相等.
的距離相等.
證明:∵![]() (已知),
(已知),
∴![]() (______),
(______),
∴![]() (______),
(______),
∵![]() (已知),
(已知),
∴![]() (______),
(______),
∵點![]() 到
到![]() 和
和![]() 的距離相等(已知),
的距離相等(已知),
∴![]() 是
是![]() 的角平分線(______),
的角平分線(______),
∴![]() (角平分線的定義),
(角平分線的定義),
∴![]() (______),
(______),
即![]() 平分
平分![]() (角平分線的定義),
(角平分線的定義),
∴點![]() 到
到![]() 和
和![]() 的距離相等(______).
的距離相等(______).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一條直線過點(0,4),且與拋物線y=![]() x2交于A,B兩點,其中點A的橫坐標是-2.
x2交于A,B兩點,其中點A的橫坐標是-2.
(1)求這條直線的解析式及點B的坐標;
(2)在x軸上是否存在點C,使得△ABC是直角三角形?若存在,求出點C的坐標,若不存在,請說明理由;
(3)過線段AB上一點P,作PM∥x軸,交拋物線于點M,點M在第一象限,點N(0,1),當點M的橫坐標為何值時,MN+3MP的長度最大?最大值是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店經銷一種健身球,已知這種健身球的成本價為每個20元,市場調查發現,該種健身球每天的銷售量y(個)與銷售單價x(元)有如下關系:y=﹣20x+80(20≤x≤40),設這種健身球每天的銷售利潤為w元.
(1)求w與x之間的函數關系式;
(2)該種健身球銷售單價定為多少元時,每天的銷售利潤最大?最大利潤是多少元?
(3)如果物價部門規定這種健身球的銷售單價不高于28元,該商店銷售這種健身球每天要獲得150元的銷售利潤,銷售單價應定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=﹣![]() x2+bx+c與坐標軸交于A,B,C三點,點A的橫坐標為﹣1,過點C(0,3)的直線y=﹣
x2+bx+c與坐標軸交于A,B,C三點,點A的橫坐標為﹣1,過點C(0,3)的直線y=﹣![]() x+3與x軸交于點Q,點P是線段BC上的一個動點,PH⊥OB于點H.若PB=5t,且0<t<1.
x+3與x軸交于點Q,點P是線段BC上的一個動點,PH⊥OB于點H.若PB=5t,且0<t<1.
(1)確定b,c的值;
(2)寫出點B,Q,P的坐標(其中Q,P用含t的式子表示);
(3)依點P的變化,是否存在t的值,使△PQB為等腰三角形?若存在,求出所有t的值;若不存在,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】勾股定理神秘而美妙,它的證法多樣,其中的“面積法”給了李明靈感,他驚喜地發現;當兩個全等的直角三角形如圖(1)擺放時可以利用面積法”來證明勾股定理,過程如下
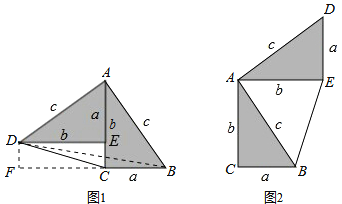
如圖(1)∠DAB=90°,求證:a2+b2=c2
證明:連接DB,過點D作DF⊥BC交BC的延長線于點F,則DF=b-a
S四邊形ADCB=![]()
S四邊形ADCB=![]()
∴![]() 化簡得:a2+b2=c2
化簡得:a2+b2=c2
請參照上述證法,利用“面積法”完成如圖(2)的勾股定理的證明,如圖(2)中∠DAB=90°,求證:a2+b2=c2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠BAC=90°,AB=AC=2,以AB為直徑的圓交BC于D,則圖中陰影部分的面積為( )

A. 1 B. 2 C. 1+![]() D. 2﹣
D. 2﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】臺風是一種自然災害,它在以臺風中心為圓心,一定長度為半徑的圓形區域內形成極端氣候,有極強的破壞力.如圖,監測中心監測到一臺風中心沿監測點B與監測點A所在的直線由東向西移動,已知點C為一海港,且點C與A, B兩點的距離分別為300km、 400km,且∠ACB=90°,過點C作CE⊥AB于點E,以臺風中心為圓心,半徑為260km的圓形區域內為受影響區域.
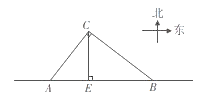
(1)求監測點A與監測點B之間的距離;
(2)請判斷海港C是否會受此次臺風的影響,并說明理由;
(3)若臺風的速度為25km/h,則臺風影響該海港多長時間?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com